傅里叶变换

任意一个函数表示成诺干个正交函数的线性组合。

时域 空间域

• x 轴是时间

• 例子

  • 信号

    • 一个物理量在时间上的变换

  • 三角函数图

频域 变换域

• x 轴是频率

• y 轴是对应频率下的增幅

时域到频域变换 #card

$F(\omega)=\int_{-\infty}^{+\infty} f(t) \cdot e^{-i \omega t} \mathrm{~d} t$

• $F(f)=\int_{-\infty}^{+\infty} f(t) \cdot e^{-i 2 \pi f t} \mathrm{~d} t$

欧拉公式

使用正弦曲线做为基，会考虑整个坐标轴情况

• g 函数是指数函数 [[拉普拉斯变换]]

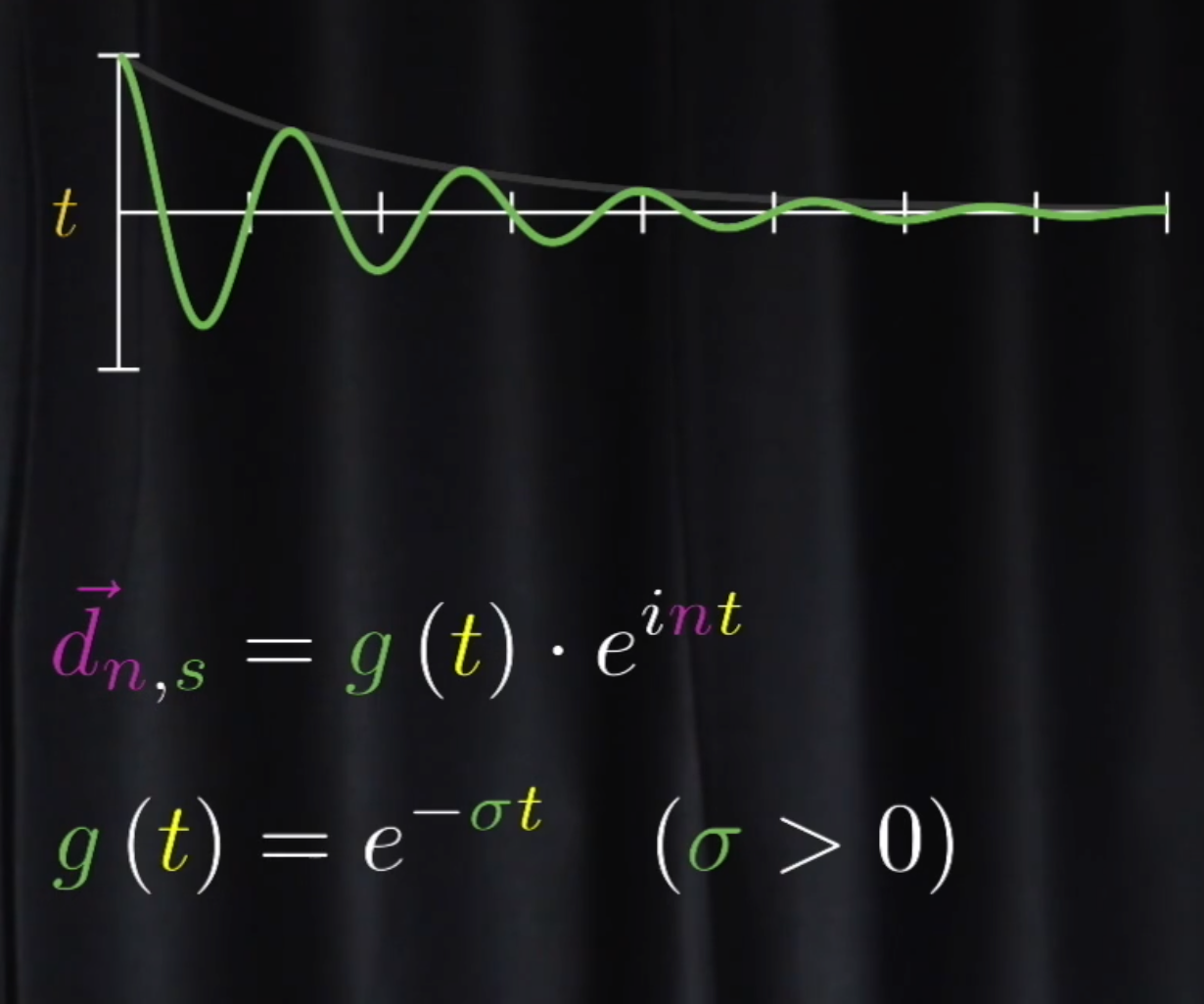
• 高斯分布做 g 函数的变换 [[Gabor Transform]]

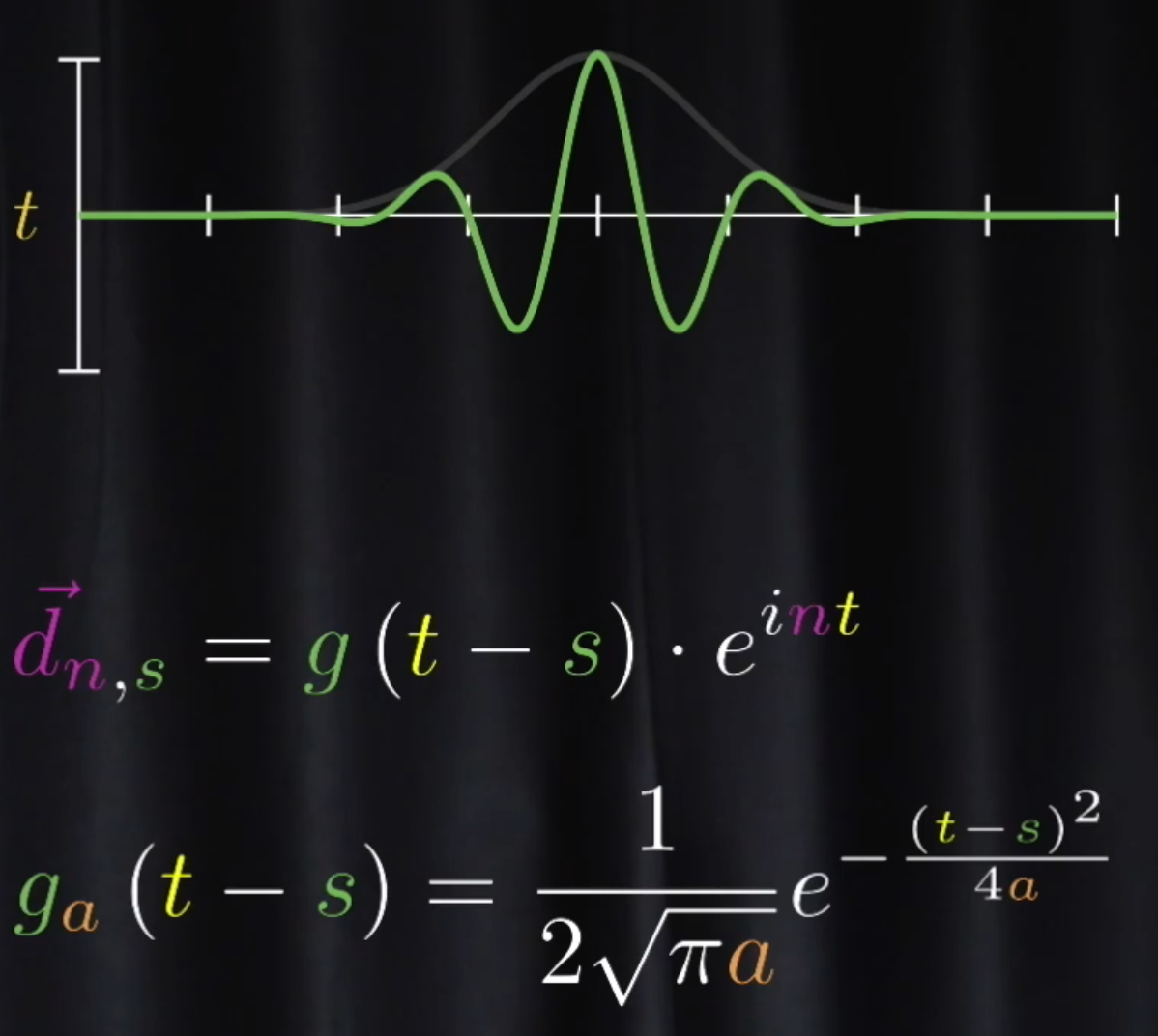
+ s 控制窗口位置

+ $\vec{d}_{n, s}=g(t-s) \cdot e^{i n t}$

$g_a(t-s)=\frac{1}{2 \sqrt{\pi a}} e^{-\frac{(t-s)^2}{4 a}} \times 2$

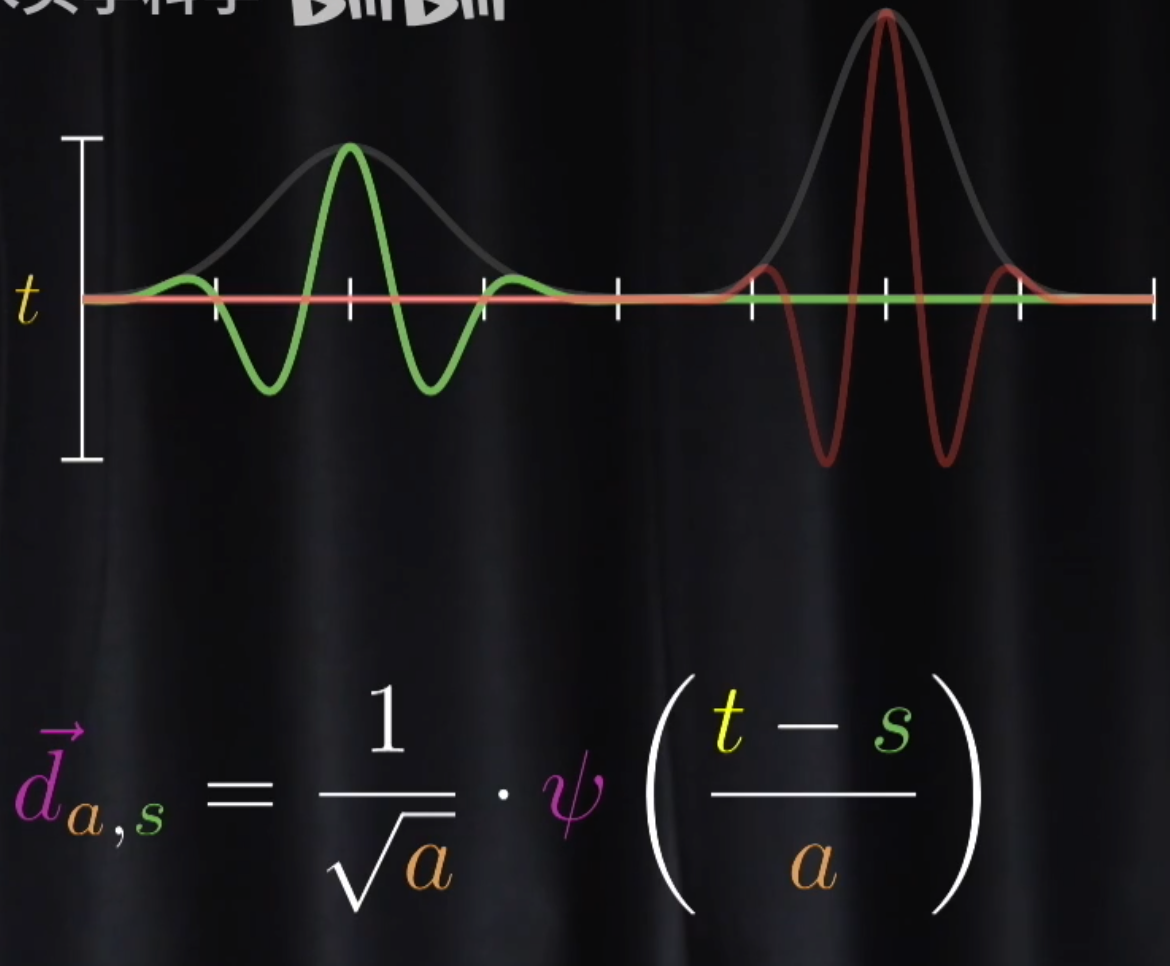
• 窗口大小不固定 [[小波变换]]