匹配法

基本形式 #card

• 匹配法就是找出对应组的相似对象并将其事实结果作为反事实结果估计

• 该方法运用能够影响结果的协变量，从对照组中选出和干预组相似的样本进行匹配，并对两个组进行比较。

匹配法成立的条件是影响结果的所有协变量均 可观测
存在多个协变量时，也可以将它们整合成一个得分进行 :-> 匹配 [[倾向性评分匹配]]。
倾向得分匹配法成立必须满足两个前提条件。#card

• 第一个前提条件是，所有会影响结果的协变量均为可转化成数值的数据。

• 第二个前提条件是所有协变量都必须用来计算倾向得分

例子：对于干预组的一件打9折的连衣裙A，可以在控制组的没打折的连衣裙中找出具有相似款式，风格，材质等属性的连衣裙B，将B的销量作为A的 反事实结果 。
匹配可以形式化如下，其中 $\hat{Y}_i$ 为单元 $i$ 的预估结果， $Y_i$ 为单元 $i$ 的事实结果， $J(i)$ 为单元 $i$ 的匹配邻居。这里包含两个问题：1）如何定义相似？2）如何挑选邻居？#card

距离度量

• 原始空间：#card

  • 我们可以基于原始的背景变量计算欧氏距离，马氏距离等常见的距离。当背景变量较少时也可以进行完全匹配，例如只有性别，年龄，城市，学历等完全相同时才匹配为邻居。

• 变换空间：#card

  • 在原始空间不一定能够找到合适的距离度量，因此我们可以将背景变量变换到其他空间，在该空间用常见的距离度量也有较好的效果，可以形式化为 $D(x_i,x_j)=\Vert f(x_i)-f(x_j)\Vert_2$ 。这里重点在于变换函数 $f$ 如何设计。

• 倾向性分：#card

  • $f(x) = e(x)$

• 线性倾向性分：#card

  • $f(x) = logits(e_i)$

• 基于预测分数：#card

  • 有点像 Domain Adaption 中对齐标签信息，使得背景变量相似的样本映射到变换空间后具有相似的事实结果，代表性方法是 HSIC-NNM。

• 基于随机映射：#card

  • 高维空间变量随机映射到低维空间后仍然可以保持原来的相似信息，代表方法是 RNNM。

• 混合方法：首先基于所有背景变量用倾向性分做一遍粗筛，然后对于关键背景变量用以下度量做一遍精筛。#card
  

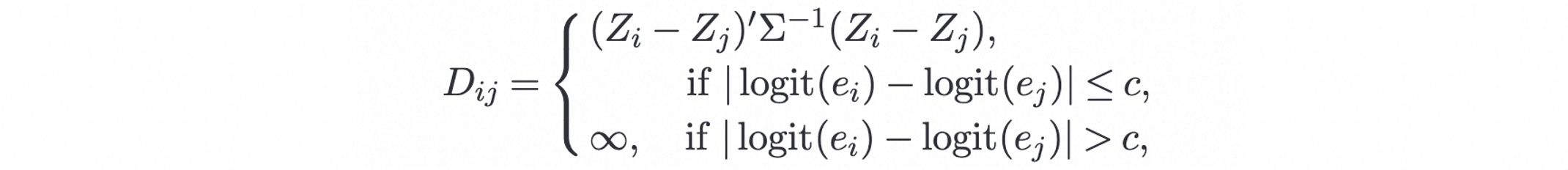
邻居选择

• 最近邻匹配：#card

  • 顾名思义取距离最近的邻居，是否有放回，匹配的数量等会影响最终的效果。当采取无放回匹配时，匹配的顺序也会影响效果。

• 分层匹配：#card

  • 将距离划分成不同区间分别匹配增加邻居的多样性。

• 完全匹配：#card

  • 匹配对应组所有样本，但是会有一个加权权重。

变量选择：#card

• 在计算距离时一般会使用所有背景变量，但是正如 D2VD 中提到的问题，背景变量中还包含其他变量，例如调整变量，工具变量等，使用这些变量会带来负向影响。