@PPO与GRPO中的KL散度近似计算
标准 [[KL Divergence]] 计算公式 $K L(q | p)=\sum_x q(x) \log \frac{q(x)}{p(x)}=\mathbb{E}_{x \sim q}\left[\log \frac{q(x)}{p(x)}\right]$
- 在实际计算中,直接计算 KL 散度可能非常困难,主要原因如下:#card
需要对所有 x 进行求和或积分,计算成本高。
计算过程中可能涉及大规模概率分布,导致内存消耗过大。
[[K1 估计器]] 计算公式 :-> $k 1=\log \frac{q(x)}{p(x)}=-\log r$
为什么是 KL 的无偏估计 #card
- $\mathbb{E}[k 1]=\mathbb{E}_{x \sim q}\left[\log \frac{q(x)}{p(x)}\right]=K L(q | p)$
K1 估计器的方差较大,因为 #card
若 $q(x)<p(x), k 1$ 可能为负值,导致估计值波动大。
若 $p(x)$ 和 $q(x)$ 差异大,$k 1$ 可能出现较大的数值变化。
[[K2 估计器]] 公式 :-> $k 2=\frac{1}{2}\left(\log \frac{p(x)}{q(x)}\right)^2=\frac{1}{2}(\log r)^2$
- K2 估计器是 有偏估计,但其方差较低,且 偏差在实证中较小,因为:#card
- K2 确保所有样本的值都是正数,使其在计算中更加稳定。
[[K3 估计器]] 公式 :-> $k 3=\frac{q(x)}{p(x)}-1-\log \frac{q(x)}{p(x)}=(r-1)-\log r=(r-1)+k 1$
K3 估计器也是 $KL(q | p)$ 的无偏估计。证明如下:#card
已知:$\mathbb{E}[k 1]=K L(q | p)$
我们只需证明:$\mathbb{E}[r-1]=0$
即:$\mathbb{E}[r]=1$
展开计算:$\mathbb{E}[r]=\mathbb{E}_{x \sim q}\left[\frac{p(x)}{q(x)}\right]=\int q(x) \cdot \frac{p(x)}{q(x)} d x=\int p(x) d x=1$
K3 估计器恒大于等于 0。证明如下 #card
设函数:$f(x)=x-1-\log x, \quad(x>0)$
求导数:$f^{\prime}(x)=1-\frac{1}{x}$
当 $0<x<1$ 时,$f^{\prime}(x)<0$ ;当 $x>1$ 时,$f^{\prime}(x)>0$ 。即,$f(x)$ 在 $x=1$ 处取最小值,且:$f(1)=1-1-\log 1=0$
所以,对于任意 $x>0$ ,均有:$f(x) \geq 0$
PPO 算法中的 KL 近似计算#card
在 GRPO(Generalized Reinforcement Policy Optimization) 算法中,KL散度是显式融入到损失函数中,近似计算采用的是 K3 估计器,如下所示:#card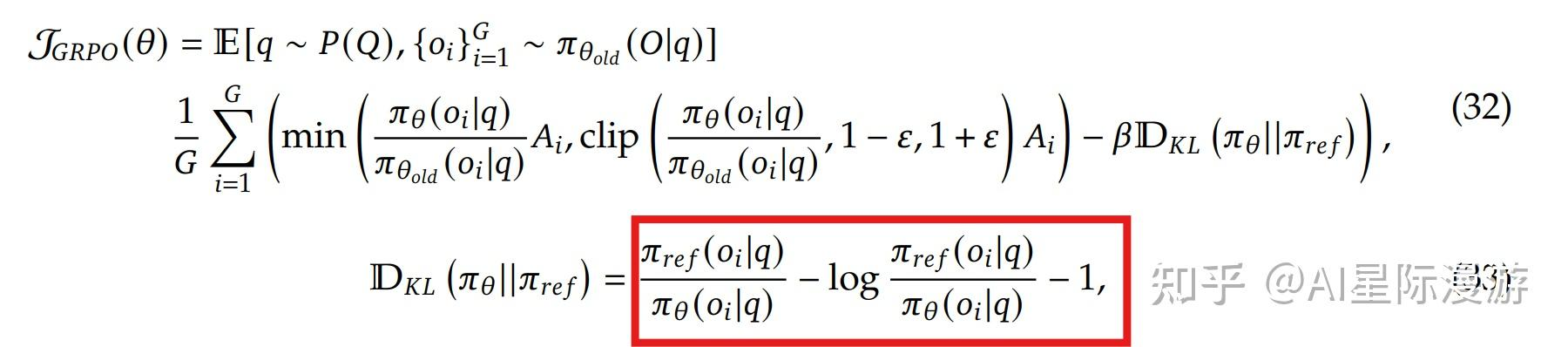
@PPO与GRPO中的KL散度近似计算
https://blog.xiang578.com/post/logseq/@PPO与GRPO中的KL散度近似计算.html