L1 和 L2 正则

梯度角度

• L1 当w大于0时，更新的参数w变小；当w小于0时，更新的参数w变大

• L2 正常的更新参数多了一项 $$\frac{w}{n}$$，当w趋向于0时，参数减小的非常缓慢，因此L2正则化使参数减小到很小的范围，但不为0。

解空间角度

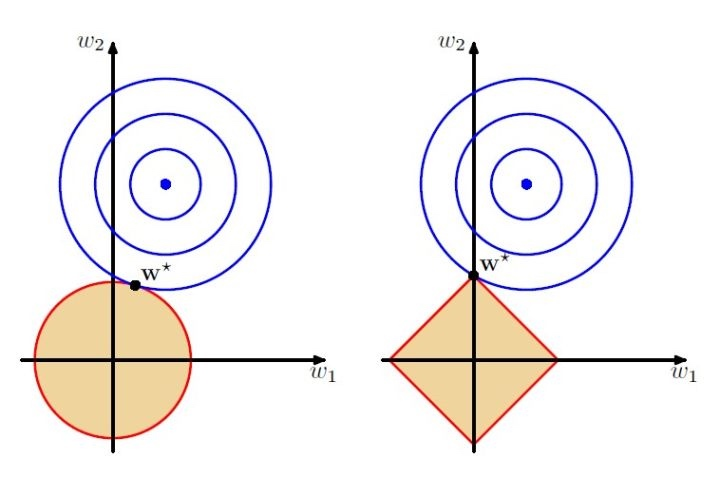
• 上图的图形给出一个直观的解释，但是需要思考细节

  • 黄色的范围是参数的空间，向 0 收缩。

  • 两个圆的交点，就是我们需要求的参数。

• L1 正则中交点有更大概率在坐标轴上，大量参数是 0 :<-> 求解出现的参数比较稀疏。

• [[为什么加入正则是定义一个解空间的约束？]]

  • [[KKT]]: $\min \sum_{i=1}^N\left(y_i-w^T x_i\right)^2$ 加入正则等价于增加 :-> 一个不等式约束条件 s.t. $\|w\|_2^2 \leq m$
    • 拉格朗日函数 :-> $\sum_{i=1}^{N}\left(y_{i}-w^{\mathrm{T}} x_{i}\right)^{2}+\lambda\left(\|w\|_{2}^{2}-m\right)$
      • 最优解 $w^*$ 和 $\lambda^*$ 满足 :-> $\nabla_w\left(\sum_{i=1}^N\left(y_i-w^{* T} x_i\right)^2+\lambda^*\left(\left\|w^*\right\|_2^2-m\right)\right)=0$
        • $\lambda^*$ 限制条件 :-> $\lambda^* \geq 0$
        • $w^*$ 对应 :-> L2正则项的优化问题的最优解条件
        • $\lambda$ 对应 :-> L2正则项前面的正则参数
        • w 的 L2 范数 不能大于 m
    • L1 和 L2 的解空间区别体现在 对应 KKT 问题的不等式条件 不同
      贝叶斯先验 [[L1和L2正则的先验分布]]

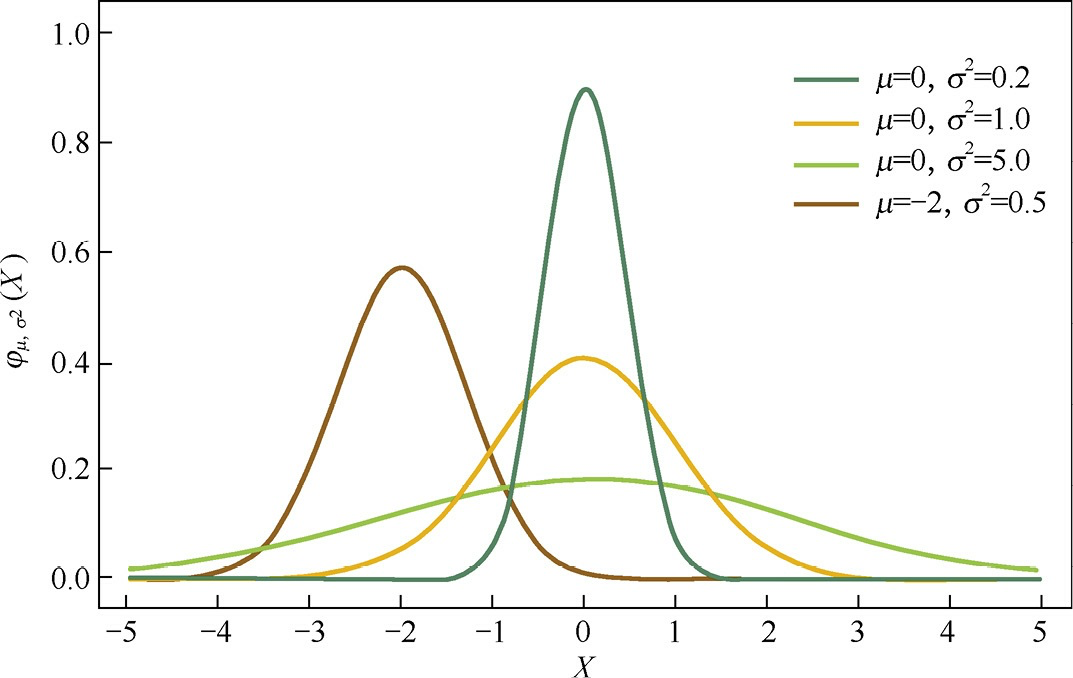
• 高斯分布 w 在极值点处平滑，w 在附近取不同值的可能性是接近的。L2 正则让 w 更接近于 0 但不会取 0。
  

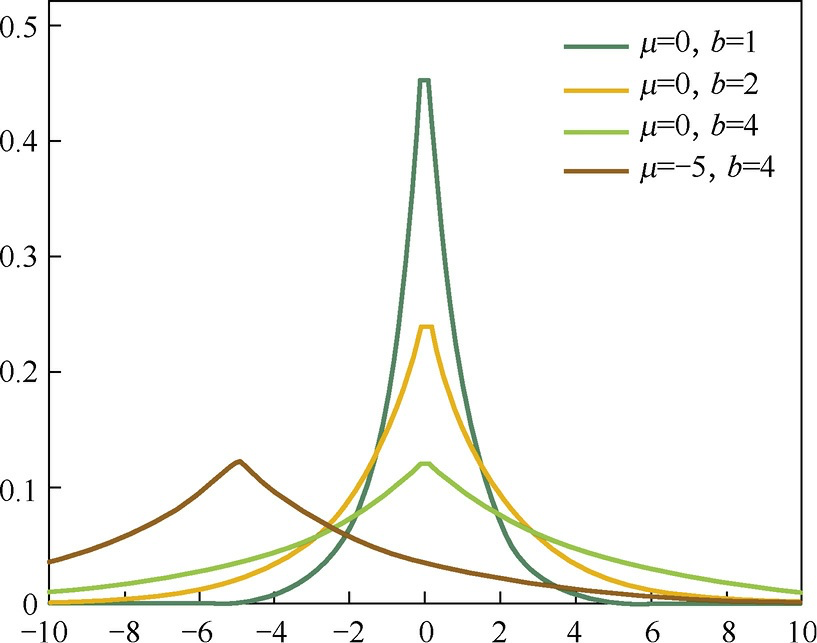
• [[Laplace Distribution]] 0 点处是一个尖峰，参数 w 取值为 0 概率更大。

  • 可以用于稀疏权值矩阵，用于特征选择，实现参数稀疏化。

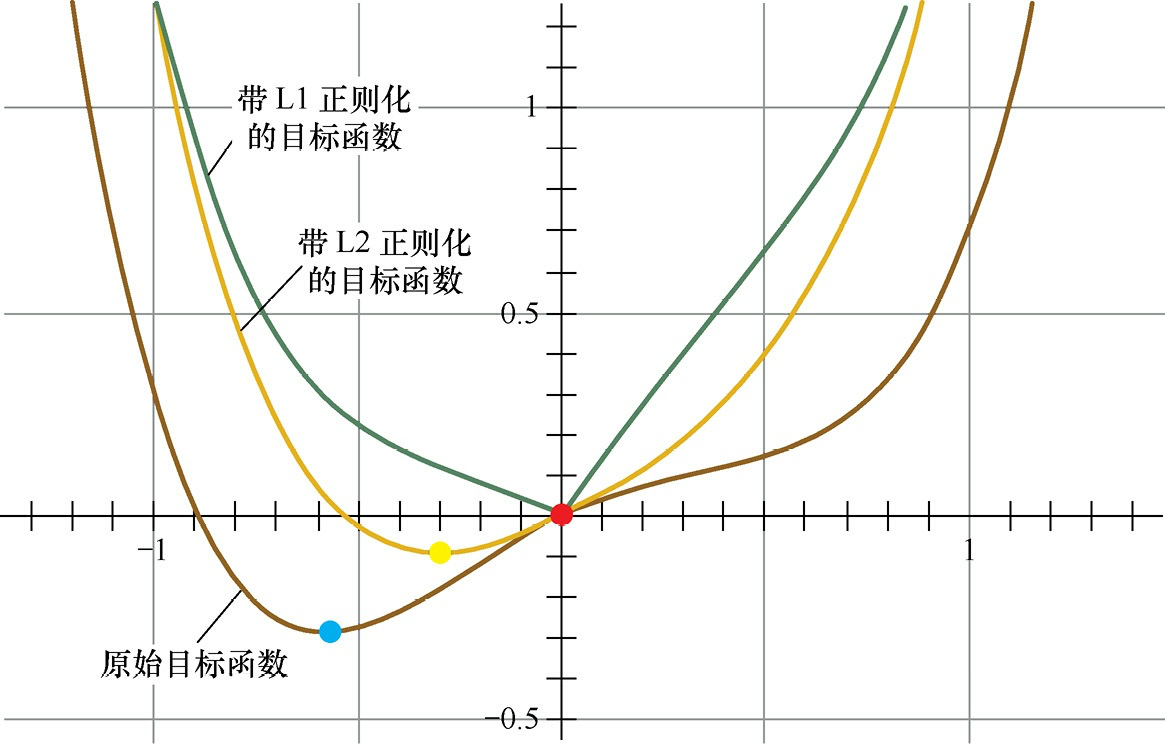
带不同正则化目标函数对比

occlusion:: eyIuLi9hc3NldHMvaW1hZ2VfMTcyNjc1MDU3MTA0NV8wLnBuZyI6eyJjb25maWciOnt9LCJlbGVtZW50cyI6W3sibGVmdCI6Mjk3Ljg0NDAwNDYwMDM0NDEsInRvcCI6OTcuMjkyMzQxMjYyMTA2MjUsIndpZHRoIjo0Ny42OTE1NTY2OTYzMjc3MywiaGVpZ2h0Ijo1MC41OTYzNjk5MzMyNzM5OSwiYW5nbGUiOjAsImNJZCI6MX0seyJsZWZ0IjozNTQuODQ1NzU5MDY4Mjk2MiwidG9wIjoyNDMuNzk2NDM0NjExNzQyMTQsIndpZHRoIjo0OS42ODg2MDY4NzY1ODQwMDQsImhlaWdodCI6MzcuNTkyMDQyMjg0MTYzOTk1LCJhbmdsZSI6MCwiY0lkIjoxfV19fQ==