Spectral Networks and Deep Locally Connected Networks on Graphs

基于空域的卷积构建 Spatial Construction

• 直接在原始图结构上执行卷积

  • 考虑 CNN 的空间局部性、多尺度特点

+ 方法

  + 按照什么条件去找中心vertex的neighbors，也就是如何确定receptive field？

    + vertex domain(spatial domain)，找出每个顶点相邻的 neighbors

    + 根据顶点的领域进行简单的聚类

  + 确定receptive field，按照什么方式处理包含不同数目neighbors的特征？

    + 卷积操作

      + $\overrightarrow{\mathbf{o}}_{j}=\sum_{i \in \mathcal{N}_{\delta}(j)} F_{i, j} \overrightarrow{\mathbf{x}}_{i}$

        + $F_{i,j}$ 是卷积核

    + 非线性层

    + 聚类

      + 通过聚类算法将 $d_{k-1}$ 个顶点聚成 $d_k$ 个簇

    + 池化层 [[Pooling]]

      + 如何根据簇内顶点向量计算每个簇的向量表示，常用有均值池化、最大池化

+ 缺点

  + 每个顶点提取出来的neighbors不同，使得计算处理必须针对每个顶点

    + 每一层降低空间分辨率，增加空间通道数

  + 提取特征的效果可能没有卷积好

+ 例子

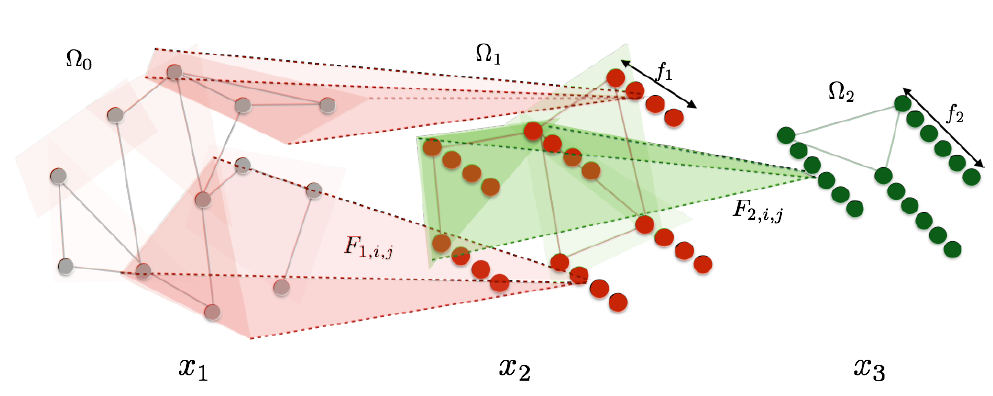
  + 第 0 层，12个顶点，一个通道

  + 第 1 层， 6个顶点，4个通道

  + 第 2 层，3 个顶点，6个通道

• 特点

  • 不需要对图结构有很高的规整性假设 regualryity assumption

  • 无法在顶点之间共享权重。

基于谱域的卷积构建 Spectral Construction

• 对图结构进行傅里叶变化，在谱域进行卷积。

• $y_{\text {output }}=\sigma\left(U g_{\theta}(\Lambda) U^{T} x\right)$

  • $g_{\theta}(\Lambda) = diag(\theta _i)$ 是卷积核

• $(f * h)_{G}=U\left(\begin{array}{lll}\hat{h}\left(\lambda_{1}\right) & & \\ & \ddots & \\ & & \hat{h}\left(\lambda_{n}\right)\end{array}\right) U^{T} f$
  中间项变成卷积核 $diag(\theta _l)$

• 问题

  • 卷积空间 局部性
    不好

  • 计算复杂度高，需要对拉普拉斯矩阵进行谱分解求解 U 以及 $Ug_{\theta}(\Lambda) U^{T}$ 的乘积

  • 每个卷积核需要 n 个参数