Tweedie Loss

$L(\hat{y})$ = :-> ${ - y \frac{\hat{y}^{1-p}}{1-p} + \frac{\hat{y}^{2-p}}{2-p}, 1<p<2}$
特点

• 非高斯分布

• y = 0，如果预测结果不为 0 ，会有损失

• 应用场景

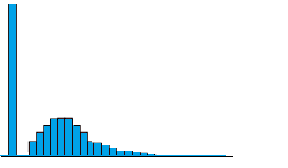
  • 奢侈品销售或者电商销售，大部分是浏览不购买，导致 0 处值非常大。

  • 如果正负样本比例差异大，但是数量充足还是可以训练。

    • 这是回归问题，取值是连续的……

  • 如果直接下采样，会破坏分布

  • 回到之前 回归问题使用什么损失函数由数据分布决定
    的问题，决定为什么会有这个损失函数

Question

• 一般什么情况下使用 Tweedie Loss $L(\hat{y})$ = :-> ${ - y \frac{\hat{y}^{1-p}}{1-p} + \frac{\hat{y}^{2-p}}{2-p}, 1<p<2}$
  ？ #card

  • 奢侈品销售或者电商销售，大部分是浏览不购买，导致 0 处值非常大。

  • 如果直接下采样，会破坏分布

Ref

• [[LightGBM/Tweedie Loss]] 实现

• M5 Forecasting - Accuracy | Kaggle

• 根据标签分布来选择损失函数 - 知乎