(FM) Factorization Machines

Factorization Machines(FM) 由日本 Osaka University 的 Steffen Rendle [1] 在 2010 年提出,是一种常用的因子机模型。

FM

假设现在有一个电影评分的任务，给定如下如所示的特征向量 x（包括用户名、当前在看的电影、已经打分的电影、时间特征、之前看的电影），预测用户对当前观看电影的评分。

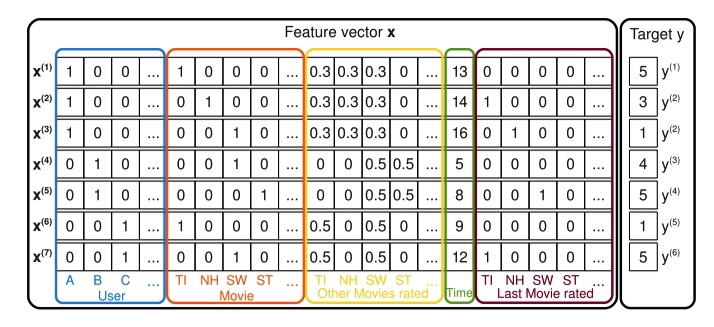
作者在线性回归模型的基础上，添加交叉项部分，用来自动组合二阶特征。

$$\hat y(x):= w_0 + \sum_{i=1}^{n} w_ix_i + \sum_{i=1}^n \sum_{j=i+1}^n \left \langle v_i,v_j \right \rangle x_ix_j$$

其中交叉特征的权重由两个向量的点积得到，可以解决没有在模型中出现的特征组合权重问题，以及减少参数数量。

$$W_{i,j}=\left \langle v_i,v_j \right \rangle = \sum_{f=1}^kv_{i,f} \cdot v_{j,f}$$

通过下面的方法来化简交叉项权重计算，算法复杂度降到线性。

$$\sum_{i=1}^n \sum_{j=i+1}^n \left \langle v_i,v_j \right \rangle x_iy_i = \frac{1}{2}\sum^k_{f=1} \left( \left(\sum_{i=1}^nv_{i,f}x_i \right)^2 - \sum^n_{i=1} v^2_{i,f} x_i^2 \right)$$

对交叉项部分的求导：

$$\frac{\partial}{\partial \theta} \hat y \left( x \right) = \begin{cases} 1, & \text{ if $\theta$ is $w_0$} \\ x_i, & \text{ if $\theta$ is ${w_i}$} \\ x_i\sum^n_{j=1} v_{j,f}x_j - v_{i,f}x_i^2, &\text{if $\theta$ is ${v_{i,f}}$} \end{cases}$$

其中 ${\sum^n_{j=1} v_{j,f}x_j}$ 与 ${x_i}$ 无关，可以在计算导数前预处理出来。

FM vs SVM

对于经典的特征组合问题，不难想到使用 SVM 求解。Steffen 在论文中也多次将 FM 和 SVM 做对比。

在考虑 SVM 的 Polynomial kernel 为 ${K(\mathbf{x}, \mathbf{z}) :=(\langle\mathbf{x}, \mathbf{z}\rangle+ 1)^{2}}$，映射

$$\begin{array}{l}{\phi(\mathbf{x}) :=\left(1, \sqrt{2} x_{1}, \ldots, \sqrt{2} x_{n}, x_{1}^{2}, \ldots, x_{n}^{2}\right.} {\sqrt{2} x_{1} x_{2}, \ldots, \sqrt{2} x_{1} x_{n}, \sqrt{2} x_{2} x_{3}, \ldots, \sqrt{2} x_{n-1} x_{n} )}\end{array}$$

SVM 的公式可以转化为：

$$\begin{aligned} \hat{y}(\mathbf{x})=w_{0}+\sqrt{2} \sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n} w_{i, i}^{(2)} x_{i}^{2} &+\sqrt{2} \sum_{i=1}^{n} \sum_{j=i+1}^{n} w_{i, j}^{(2)} x_{i} x_{j} \end{aligned}$$

论文中提到一句上面的公式中 ${w_{i}}$ 和 ${w_{i,i}}$ 表达能力类似，我猜这也是为什么 FM 中没有自身交叉项的原因吧。

FM 相比于 SVM 有下面三个特点：

1. SVM 中虽然也有特征交叉项，但是只能在样本中含有相对应的特征交叉数据时才能学习。但是 FM 能在数据稀疏的时候学习到交叉项的参数。
2. SVM 问题无法直接求解，常用的方法是根据拉格朗日对偶性将原始问题转化为对偶问题。
3. 在使用模型预测时，SVM 依赖部分训练数据（支持向量），FM 模型则没有这种依赖。

Rank

FM 用来做回归和分类都很好理解，简单写一下如何应用到排序任务中。以 pairwise 为例。假设排序结果有两个文档 ${x_i}$ 和 ${x_j}$，显然用户点击文档有先后顺序，如果先点击 ${x_i}$，记 label ${y_{ij}=1}$，反之点击 ${x_j}$，label ${y_{ij}=0}$。模型需要去预测 ${\hat y_{ij} = sigmoid(\hat y_i - \hat y_j)}$。

参考逻辑回归，用最大似然对参数进行估计，得到损失函数为 ${L=\log(1+\exp(-(\hat y(x_i)-\hat y(x_j))}$。优化过程和前面提到类似。

NFM

NFM 和 AFM 两篇论文是同一个作者写的，所以文章的结构很相近。

FM 模型由于复杂度问题，一般只使用特征二阶交叉的形式，缺少对 higher-order 以及 non-liner 特征的交叉能力。NFM 尝试通过引入 NN 来解决这个问题。

NFM 的结构如下：第一项和第二项是线性回归，第三项是神经网络。神经网络中利用 FM 模型的二阶特征交叉结果做为输入，学习数据之间的高阶特征。与直接使用高阶 FM 模型相比，可以降低模型的训练复杂度，加快训练速度。

$$\hat{y}_{N F M}(\mathbf{x})=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+f(\mathbf{x})$$

NFM 的神经网络部分包含 4 层，分别是 Embedding Layer、Bi-Interaction Layer、Hidden Layers、Prediction Score。

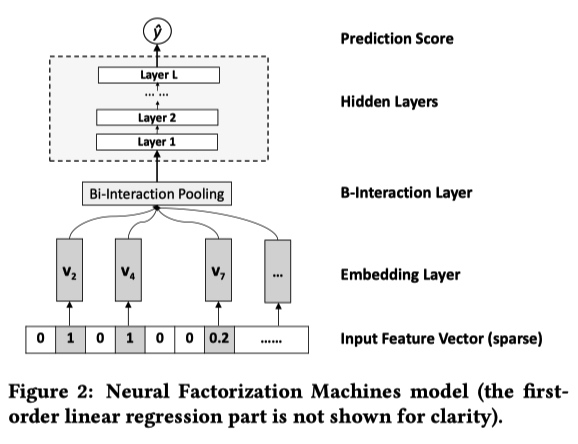
• Embedding Layer 层对输入的稀疏数据进行 Embedding 操作。最常见的 Embedding 操作是在一张权值表中进行 lookup ，论文中作者强调他们这一步会将 Input Feture Vector 中的值与 Embedding 向量相乘。
• Bi-Interaction Layer 层是这篇论文的创新，对 embedding 之后的特征两两之间做 element-wise product，并将结果相加得到一个 k 维（Embeding 大小）向量。这一步相当于对特征的二阶交叉，与 FM 类似，这个公式也能进行化简：

$$f_{B I}\left(\mathcal{V}_{x}\right)=\sum_{i=1}^{n} \sum_{j=i+1}^{n} x_{i} \mathbf{v}_{i} \odot x_{j} \mathbf{v}_{j} =\frac{1}{2}\left[\left(\sum_{i=1}^{n} x_{i} \mathbf{v}_{i}\right)^{2}-\sum_{i=1}^{n}\left(x_{i} \mathbf{v}_{i}\right)^{2}\right]$$

• Hidden Layers 层利用常规的 DNN 学习高阶特征交叉
• Prdiction Layer 层输出最终的结果：

$$\begin{aligned} \hat{y}_{N F M}(\mathbf{x}) &=w_{0}+\sum_{i=1}^{n} w_{i} x_{i} +\mathbf{h}^{T} \sigma_{L}\left(\mathbf{W}_{L}\left(\ldots \sigma_{1}\left(\mathbf{W}_{1} f_{B I}\left(\mathcal{V}_{x}\right)+\mathbf{b}_{1}\right) \ldots\right)+\mathbf{b}_{L}\right) \end{aligned}$$

实验结果：

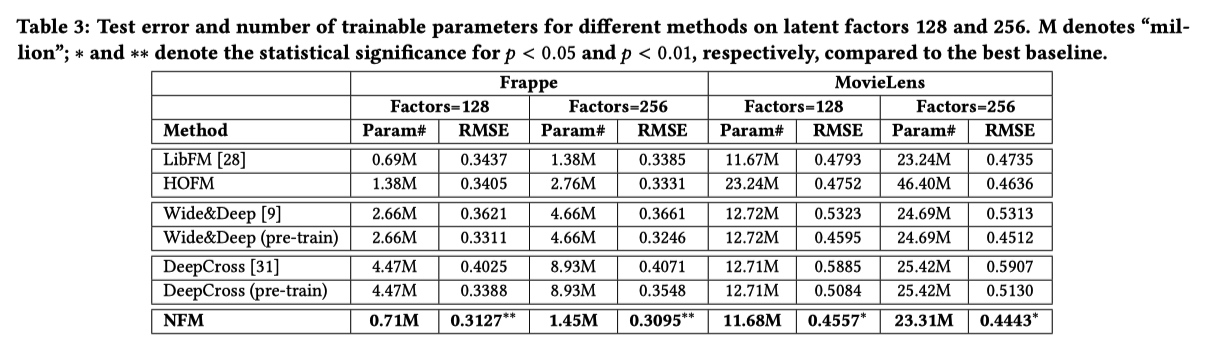
AFM

AFM(Attentional Factorization Machine), 在 FM 的基础上将 Attention 机制引入到交叉项部分，用来区分不同特征组合的权重。

$$\hat{y}_{A F M}(\mathbf{x})=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\mathbf{p}^{T} \sum_{i=1}^{n} \sum_{j=i+1}^{n} a_{i j}\left(\mathbf{v}_{i} \odot \mathbf{v}_{j}\right) x_{i} x_{j}$$

单独看上面公式中的第三项结构：

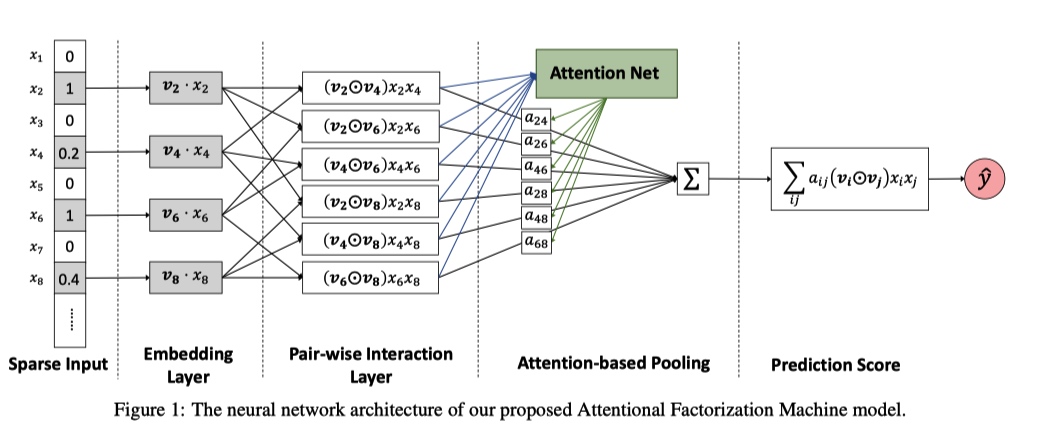
• Embedding Layer 与 NFM 里面的作用一样，转化特征。
• Pair-wise Interaction Layer 是将特征两两交叉，如果对这一步的结果求和就是 FM 中的交叉项。
• Attention 机制在 Attention-based Pooling 层引入。将 Pair-wise Interaction Layer 中的结果输入到 Attention Net 中，得到特征组合的 score ${a_{i j}^{\prime} }$，然后利用 softmax 得到权重矩阵 ${a_{ij}}$。

$$\begin{aligned} a_{i j}^{\prime} &=\mathbf{h}^{T} \operatorname{Re} L U\left(\mathbf{W}\left(\mathbf{v}_{i} \odot \mathbf{v}_{j}\right) x_{i} x_{j}+\mathbf{b}\right) \\ a_{i j} &=\frac{\exp \left(a_{i j}^{\prime}\right)}{\sum_{(i, j) \in \mathcal{R}_{x}} \exp \left(a_{i j}^{\prime}\right)} \end{aligned}$$

• 最后将 Pair-wise Interaction Layer 中的二阶交叉结果和权重矩阵对应相乘求和得到 AFM 的交叉项。

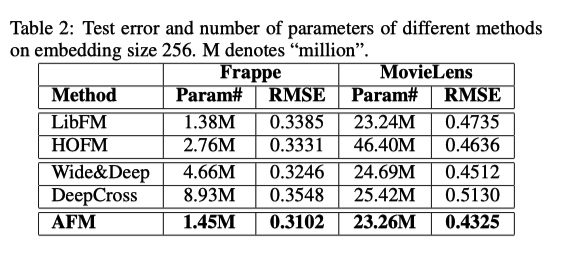
和前一节的实验结果对比，AFM 效果比 NFM 要差一些。这大概就能说明为什么论文中提到 NFM，但是最后没有把 NFM 的结果贴出来，实在是机智。又回到，发论文是需要方法有创新，还是一味追求 state-of-the-art。

参考资料

• 深入浅出Factorization Machines系列 | Kubi Code’Blog
• FM模型在LTR类问题中的应用 - 知乎