@LLM实践--理解Language Model是如何到PPO的 理论篇

链接：LLM实践–理解Language Model是如何到PPO的 理论篇 - 知乎

在下面的文章里，我们约定，在语言模型的场景下：$X \sim \mathcal{D}$ 表示一条文本X采样自数据集D #card

• 假设我们数据集D只有下面4条文本。

  • $X_1=$ 中国的首都是哪里？北京。

  • $X_2=$ 中国的首都是哪里？中国的首都是北京。

  • $X_3=$ 中国的首都是哪里？中国的首都不是广州和武汉，是北京。

  • $X_4=$ 中国的首都是哪里？中国的首都不是广州，是北京。

• 约定 $x_t$ 表示一条文本中的第 t 个token，$x_{<t}$ 表示所有 t 之前的token。

奖励模型作用 :-> 给定一条文本X，奖励模型可以给这个文本打分 $r_X$ ，表示这条文本在人类定义的偏好下的好坏。

• 奖励模型训练使用这个loss函数： $\mathcal{L}_{\text {reward }}=-\log \sigma\left(r_{X_{\text {chosen }}}-r_{X_{\text {rejected }}}\right)$ #card

  • 其中 $r_{X_{\text {chosen }}}$ 和 $r_{X_{\text {rejected }}}$ 分别表示好，坏文本的奖励分数。一般取每个文本最后一个token的 logits，乘一个shape＝［embedding＿dim，1］的矩阵，映射成一个1维分数。

  • 从奖励模型的loss上看，模型建模的是相对分数，而不是绝对分数，实际也是如此。

  • 不同domian的分数区间是不同的，很难找到一个统一的阈值划分好坏，所以用的时候一般要伴随使用norm（或者baseline）。

[[@PPO与GRPO中的KL散度近似计算]] 要点

• 一个是KL散度的方向：假设需要训练的模型是分布 A ，作为基准的分布是分布 B ，从训练分布中采样的 $K L(A \| B)$ 称为正向KL，从基准分布中采样的 $K L(B \| A)$ 称为反向 KL 。 #card

  • 正向 KL 有模式坍塌，反向 KL 会更全面的覆盖基准分布，但是部分概率拟合偏差较大。

  • 在Post－train之前的阶段我会优先使用反向KL，比如预训练，持续训练，蒸馏，因为此时模型学习的目标是尽可能全面的覆盖自然世界知识。

  • 在Post－ train我一般优先尝试正向KL，这个时候模式坍塌是不可避免的，也是可接受的。

• 一个是KL散度的估计方式

  • 为什么有时候使用 [[K2 估计器]] 和 [[K3 估计器]] 替代 [[K1 估计器]] #card

    • 蒙特卡洛估计是无偏的，当采样趋近于无穷的时候估计的就是KL散度本身，但是在采样数量少时方差太大。

    • 离散KL散度本来是非负的，但使用蒙特卡洛估计时值可能为负。所以一个简单的考虑是让估计值非负来减小方差，绝对值估计或 [[K2 估计器]] 。

加权语言模型

• 观察我们的数据集D，既然我们有一个能给文本打分的reward模型，不妨假设模型会这样给每个条数据打质量分：#card

  • $X_1$ 虽然正确，但是太简短了，$r_{X_1}=1$

  • $X_2$ 的回答主谓宾完整，质量好于第一条，质量分 $r_{X_2}=1.5$

  • $X_3$ 虽然也是正确的，但是＂不是广州和武汉＂明显是冗余的，质量分 $r_{X_3}=0.5$

  • $X_4$ 正确的且比 $X_3$ 废话少一点 $r_{X_4}=0.7$

• 既然训练语料有了质量分，那么一个自然的想法就是让质量更高的文本在训练时的loss重要性高一些，反之则低一点。那么我们可以优化一下语言模型loss，改写成下面的形式：#card

  • $\mathcal{L}_{l m}=r_X \log P(X)=r_X \sum_{t=1}^T \log P\left(x_t \mid x_{<t}\right)$

  • 只要保证r不小于0，新loss函数优化得到的模型就依旧是语言模型。

  • 加权loss等价于对数据进行上、下采样。r=0.5等于在batch中下采样一倍，2等价于上采样一倍。所以只要数据集没有问题，加权loss训练的模型也不会崩。（这是理论上的情况，在实际中rejection sampling连加权都没有，也能给模型训崩，这个我们放在实验篇讨论）

Policy-base 强化学习

• 基于策略的强化学习优化目标和加权语言模型 loss 对比 #card

  • 形式上一致

    • 强化学习 $J\left(\pi_\theta\right)=E_{\tau \sim \pi_\theta}\left[R(\tau) \log P_\theta(\tau)\right]$

    • 语言模型 $\mathcal{L}=E_{X \sim \mathcal{D}}\left[r_X \log P(X)\right]$

  • 区别是一个数据数据采样自模型，一个采样自数据集

过程监督

• 如何奖励模型能对每一个 token 打分，加权语言模型 loss 改写成 #card

  • $\mathcal{L}=\sum_{t=1}^T r_t \log P\left(x_t \mid x_{<t}\right)$
  • 把 $r_X$ 移动到求和符号里面变成针对每个token的细粒度分数 $r_t$

• 一旦计算token级别的权重，这个loss优化出来模型就已经不是统计意义上的语言模型了，因为这是对每个token做不同的上、下采样。#card

  • 通俗理解：把一句话说两遍这句话还是自然语言，但是把一句话话中的某个字说丙扁这就不不是正常的语言了。另外，就算是文本级别的权重，如果取负值，那么优化的目标将不再是最大化对数似然，自然模型也不是语言模型。

  • 一旦loss是非语言模型loss，训练就有可能崩溃，因为此时模型的优化目标并不是“模型依概率采样出一句话”，优化目标和我们的采样行为出现了gap。

  • 此时就需要在基础loss上引入KL散度约束。此刻起优化目标彻底脱离“最大化数据的对数似然”，变为“最大化奖励的期望”。

  • 在这之后我会称呼我们正在训练的这个用来说话的模型为策略模型。

• $\mathcal{L}=\sum_{t=1}^T r_t \log P\left(x_t \mid x_{<t}\right)$
  学习目标的意义是 :-> 当采样一个token的分数 rt 为正，就会增加这个token的概率，分值越高增加的程度就越高。反之如果 rt 为负，则减小这个token的概率。

  • 这个目标包含的马尔可夫假设 #card

    • 即当token序列为 $x_{<t}$ ，采样这个动作 $P\left(x_t \mid x_{<t}\right)$ 只影响 $x_{\leq t}$ 的奖励，只要 $x_{\leq t}$ 的奖励 $r_t$ 高，$P\left(x_t \mid x_{<t}\right)$ 就好。

    • 马尔可夫假设是个很强的假设，很少有这么理想的情况

• $X_3=$ 中国的首都是哪里？中国的首都不是广州和武汉，是北京。
  中一个“不”字不仅让“中国的首都不”的奖励降低，还让后面“是广州和武汉”这么多token帮着往回拐。所以采样的token不仅应该对自己负责，还应该对后续token的奖励负责。将 loss 改成 #card

  • $G\left(x_t\right)=\sum_{i=t}^T r_i$，$\mathcal{L}=\sum_{t=1}^T G\left(x_t\right) \log P\left(x_t \mid x_{<t}\right)$

• $G\left(x_t\right)=\sum_{i=t}^T r_i$，$\mathcal{L}=\sum_{t=1}^T G\left(x_t\right) \log P\left(x_t \mid x_{<t}\right)$
  loss 的含义 #card

  • 当采样一个token $x_t$ 后，这个token之后所有token的总奖励分数 $G\left(x_t\right)$ 为正，就会增加这个token的概率，分值越高增加的程度就越高。反之则降低这个token的概率。

  • 在强化相关的算法中，我们会看到很多 $\sum_{i=t}^T$ 而不是更常见的 $\sum_{i=1}^T$ ，基本都是源于这种＂向后负责＂的思想。

• 再进一步，一个token对后续每个token负的责也不都是一样的，直觉上应该是距离当前位置越远，token对其负责越少。所以我们改造一下奖励的累计方法：#card

  • $G\left(x_t\right)=\sum_{i=t}^T \gamma^{i-t} r_i$

  • $\gamma$ 是一个0－1之间的超参，越大表示对后续token负责越多，趋近于 0 表示不对后续负责， 1 表示对后续负全部责任。这个改造后的累计函数就是我们之后实际使用的累计函数，在强化中也称为回报（return）。

Baseline

#card 观察图中给出的例子，由于这句话整体是正确的，所以虽然有一些废话token分数不高，但也都是正的。相当于所有token的概率都在增加，只不过不好的token增加的慢一点。这样只有等到其他更好的token概率足够高了，才能消灭掉不好的token。显然这样的学习效率很低，甚至可以说是错误的，这些错误token的概率就不应该增加。所以我们可以给这些分数做一个中心化，全部减去一个值，让分数有正有负，更明显的区分出好坏，公式可以表示为：
+ $\mathcal{L}=\sum_{t=1}^T\left[G\left(x_t\right)-b\right] \log P\left(x_t \mid x_{<t}\right)$

+ 减去的这个值，我们就称它为baseline。之所以叫baseline，是因为这是一句话的“基准”，它表示了一句话的平均好坏，如果这个句子是模型采样生成的，则也表示这个模型现有的平均能力。

• 在很多地方，我们会看到说减去baseline的作用是降低方差。哪里来的方差，为什么要降低方差？#card

  • 在强化的训练过程中，训练使用的文本是采样出来的。假设我每次都采样两条进行训练，某一次采样出了 $X_2$ 和 $X_3, ~ X_2$ 完全正确，每个token都是1．5分。

    • 那么训练时＂中国的首都－＞是＂的概率以 1.5 倍的强度提升，＂中国的首都－＞不＂以 0.5 倍的强度提升，经过softmax归一化以后，相当于在降低＂不＂的概率，模型整体的学习方向还是正确的。

  • 但是如果我只采样一条数据训练，且不幸采到了 $X_3$ ，那么＂不＂的概率将提升，模型的学习方向是错误的。这并不是说采样采的不对，也不是奖励模型打分错了。

  • 而是当采样次数不够多时，分数无法准确的反应奖励模型真正希望模型去改进的方向（不是＂不是广州和武汉＂是错的，而是奖励模型更想要不废话的答案）。

  • 这个奖励模型希望我们改进的方向是期望，而采样与这个期望的距离就是我们所说的方差。在micro－batch梯度下降这种优化方式下，过大的方差会导致模型无法收敛。

既然减去baseline作用这么大，下面我们就看看这个baseline应该怎么确定。一个朴素的想法是，用每个token的平均分作为baseline。

+ 比如图中这些token的平均分是0.76，那么减去之后每个token的分数变成：#card
  + 这样该正的正，该负的负，更符合我们的期望了。

+ 但是这么做有个问题，如果仅使用每条数据自己的均值，就意味着一个句子中的token必定有正有负。#card
  + 这会导致好句子中有部分token的概率会下降，坏句子还是有一部分token概率会上升。

  + 为了更加准确的估算这个baseline，我们应该将视野扩大，不仅关注一个token在一条数据中的相对好坏，更要从整个数据集的角度看一个token是好是坏。

在统计学中，整体的角度就是指期望。我们可以尝试计算文本中每个token的期望回报 $E\left[G\left(x_t\right)\right]$ 。用数据集D举例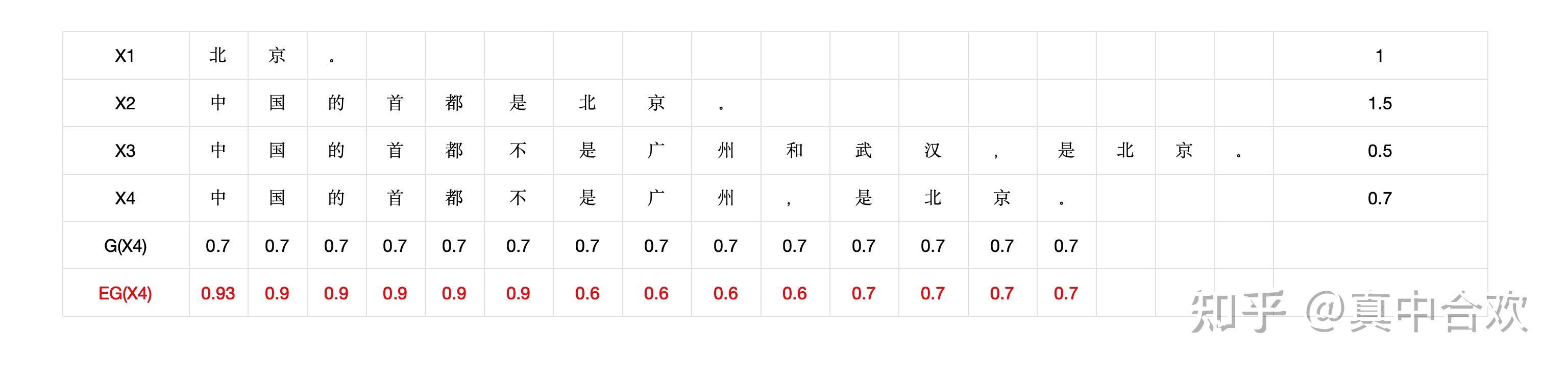说明一下这个期望分数是怎么算出来的：

+ 上表是我们数据集中的4条数据。最后一列是在最开始＂加权语言模型＂这一节中给出的文本级别的分数。#card
  + 为了好算，我假设一句话中每个token的回报都等于这句话的reward，也就是 $G\left(x_t\right)=r_T$

  + （这个假设等价于只给最后一个token打分，其他都是 0 ，并且 $\gamma$ 为 1 。

  + 这是可以实现的假设，并且也确实是实际会用到的一个假设）。

+ 计算 $X_4$ 中每个token的期望回报 $E\left[G\left(x_t\right)\right]:$

  + $E\left[G\left(x_1^4\right)\right]=E[G( 中 )]$ ，这里需要理解的一点是 $E\left[G\left(x_t\right)\right]$ 和 $G\left(x_t\right)$ 是错位的关系。#card
    + $G\left(x_t\right)$ 表达的是采样了 $x_t$ 后的回报。

    + 而 E 是期望，期望就意味着是取遍了 $x_t$ 所有可能的值后计算出的平均，它反应的其实是 $x_t$ 的前缀 $x_{<t}$ 的回报。

    + G （中）的前缀为空，所以就是整个数据集的均分 $=\frac{1+1.5+0.7+0.5}{4} \approx 0.93$

  + $E\left[G\left(x_2^4\right)\right]=E[G( 中国 )]$ ，#card
    + 也就是计算所有第 1 个token为＂中＂的数据的平均回报。

    + X2， X3，X4三条数据满足要求，所以平均回报是 $\frac{1.5+0.7+0.5}{3}=0.9$

  + $E\left[G\left(x_3^4\right)\right]=E[G( 中国的 )]$ #card
    + ，也就是计算所有前 2 个token为＂中国＂的数据的平均回报。

    + $\mathrm{X} 2, ~ \mathrm{X} 3, ~ \mathrm{X} 4$ 三条数据满足要求，平均回报是 $\frac{1.5+0.7+0.5}{3}=0.9$

  + $E\left[G\left(x_7^4\right)\right]=E[G(中国的首都不是)]$ ，#card
    + 这个时候只剩下X3，X4满足要求，平均回报＝ $\frac{0.7+0.5}{2}=0.6$

  + #card $E\left[G\left(x_{11}^4\right)\right]=E[G(中国的首都不是广州，是)]$ ，
    + 这个时候只剩下X4满足要求，平均回报 $=0.7$

  + 观察X4，会发现前几个token＂中国的首都＂都是对的，但是减去期望后分数却是负的 -0.2 。这种不合理来自于#card
    + 我们将 $\gamma$ 设定为 1 。这就导致＂中国的首都＂几个字要为后面的＂不是．．．＂负全部责任。

• 当使用期望作为baseline时，策略模型的loss函数写成：$\mathcal{L}=\sum_{t=1}^T\left[G\left(x_t\right)-E\left[G\left(x_t\right)\right]\right] \log P\left(x_t \mid x_{<t}\right)$

  • 理解一下这个loss函数： #card

    • $G\left(x_t\right)$ 表示的是采样了 $x_t$ 后的句子有多好。

    • $E\left[G\left(x_t\right)\right]$ 表示还没有采样 $x_t$ 时前缀有多好。

    • 如果采样 $x_t$ 后句子比采样之前更好（差值为正），就说明这个采样是好的，则增加概率，反之则减小概率。

  • 这个loss是理想的目标，但是在实际RLHF训练的过程中，我们无法计算 $E[G(x)]$ ，因为#card

    • RLHF时answer都是实时生成的。

    • 只有SFT，RS，DPO这种固定训练集的算法能计算出整个数据集的期望。

    • 没有办法计算就只能想办法近似。

• $\mathcal{L}=\sum_{t=1}^T\left[G\left(x_t\right)-B\left(x_t\right)\right] \log P\left(x_t \mid x_{<t}\right)$，用函数 $B(x)$ 来近似计算 $E[G(x)]$

  • 近似函数可以怎么设计 #card

    • 用贪婪采样的句子奖励来近似模型的＂平均能力＂：$B(x)=r_{X_{M A X}} \sim E[G(X)]$ ，这就是ReMAX。

    • 可以对一个prompt采样多个answer $\left(X_1, X_2, \ldots X_G\right)$ ，然后用平均奖励来近似： $B(x)=\frac{\sum_{i=1}^G r_{X_i}}{G} \sim E[G(X)]$ ，这就是GRPO。

    • 如果在计算平均奖励时，＂扣掉＂正要训练的这条数据，计算除此之外其他文本的奖励均值，就是RLOO。

  • 这种基于采样的近似方法有个特点，因为采样就会导致新的baseline answer $X_{\text {baseline }}$ 和我们要训练的数据长度不一致，因此没有办法按位对齐回报和baseline。#card

    • 所以这一类算法的 $G\left(x_t\right)$ 可以带脚标 t ，表示每个token的回报不同，但是 $B(x)$ 都是不带脚标 t 的，算整个 answer的reward。

• 有这么多种baseline的选择，那种好呢？一般评判baseline可以用两个指标：#card

  • 期望和方差。好的baseline应该不改变原始优化目标梯度的期望，并且能够减小方差。

• 是否能够不改变梯度期望比较好证明：#card

  • $\begin{aligned} E \nabla_\theta \mathcal{L} & =E \nabla_\theta \sum_{t=1}^T\left[G\left(x_t\right)-B\left(x_t\right)\right] \log P\left(x_t \mid x_{<t}\right) \\ & =\sum_{t=1}^T\left[E \nabla_\theta G\left(x_t\right) \log P\left(x_t \mid x_{<t}\right)-E \nabla_\theta B\left(x_t\right) \log P\left(x_t \mid x_{<t}\right)\right]\end{aligned}$

  • 只需要证明后面一项 $E \nabla_\theta B\left(x_t\right) \log P\left(x_t \mid x_{<t}\right)=0$ ，就能说明没有改变期望。用一下上文提到的对数求导技巧：

    • $$$$

E \nabla_\theta B\left(x_t\right) \log P\left(x_t \mid x_{<t}\right) & =B\left(x_t\right) E \nabla_\theta \log P\left(x_t \mid x_{<t}\right) \
& =B\left(x_t\right) \sum P\left(x_t \mid x_{<t}\right) \nabla_\theta \log P\left(x_t \mid x_{<t}\right) \
& =B\left(x_t\right) \sum \nabla_\theta P\left(x_t \mid x_{<t}\right) \
& =B\left(x_t\right) \nabla_\theta \sum P\left(x_t \mid x_{<t}\right) \
& =B\left(x_t\right) \nabla_\theta 1 \
& =0
\end{aligned}

+ 也就是说只要 $B\left(x_t\right)$ 与 $\nabla_\theta, E_{x_t \sim P\left(x_t \mid x_{<t}\right)}$ 无关，可以从求导和期望符号里提出来，这一项就为 0 。 + 比如ReMax中， b 是贪婪采样的answer奖励 $r_{X_{M A X}}$ 。 $X_{M A X}$ 和正在训练的句子是无关的，奖励模型也无关，所 B 就可以提到前面。 + 再比如RLOO，b是除训练文本之外的其他文本的奖励均值，所以也可以提出来。 + 但是GRPO计算时，b是包含正在训练的文本的奖励均值，就提不出来。 + 至于方差是否降低则各有各的证明方法，这就麻烦去看各个论文的原始推导吧。 ## 价值函数 + 除了这种用采样来逼近 $E[G(x)]$ 的思路，还有另一种深度学习中也很常见的思路：算不出来的东西，就用 **模型** 去拟合。 + $\mathcal{L}=\sum_{t=1}^T\left[G\left(x_t\right)-V\left(x_t\right)\right] \log P\left(x_t \mid x_{<t}\right)$，用一个模型去拟合 $G$ 的期望 $V_\zeta(x) \sim E[G(x)]$ + V在强化学习中称为 **状态价值函数** ，模型称为critic模型。在训练策略模型时，critic是不训练的，可以视为常数baseline。 + 那critic模型怎么训练呢？critic模型是在预测 $E[G(x)]$ ，这是一个典型的回归任务，那么就可以用 :-> 均方差损失来优化 $\mathcal{L}=\sum_{t=1}^T \frac{1}{2}\left(E\left[G\left(x_t\right)\right]-V\left(x_t\right)\right)^2$ + 这里又有 $E[G(x)]$ ，所以还是老办法，用采样来近似，#card + 这不过这里不需要向上面那样既采样训练用的answer，又采样baseline的answer了，直接用训练answer就可以了： + $\mathcal{L} \approx \frac{1}{2 N} \sum_{i=1}^N \sum_{t=1}^T\left(G\left(x_t^i\right)-V\left(x_t^i\right)\right)^2$ + 这个训练目标理论上是可行的，但是实际训练时这种方法比较难优化。 + id:: 67ffd3f6-13d1-49bf-9fa9-e767d9c30d2b

V\left(x_t\right) \sim E\left[G\left(x_t\right)\right]=E\left(r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\ldots+\gamma^{T-t} r_T\right)

#card + $V\left(x_t\right)$ 需要去拟合的这个 $E\left[G\left(x_t\right)\right]$ 是 r 的累加，和所有随机采样的 $x_t, x_{t+1}, \ldots, x_T$ 都有关。这里随机变量太多，比较难优化。这就相当于diffusion 模型从 $z^t$ 一步预测所有 $z^{t-1}, \ldots z^0$ ，语言模型从 $x_t$ 一步预测出 $x_{t+1}, \ldots x_T$ 。语言模型的做法是只预测下一个 token，那这里我们也想办法让V只预测一步。 + $G\left(x_{t+1}\right)$ 的表达式为： +

G\left(x_{t+1}\right)=r_{t+1}+\gamma r_{t+2}+\ldots+\gamma^{T-t-1} r_T

+ 带入 $G\left(x_t\right)$ 的表达式： +

G\left(x_t\right)=r_t+\gamma G\left(x_{t+1}\right)

$$+ 再代入到 V 的公式中： +$$

\begin{aligned}
V\left(x_t\right) \sim E\left[G\left(x_t\right)\right] & =E\left(r_t+\gamma G\left(x_{t+1}\right)\right) \
& =E\left(r_t\right)+\gamma E\left[G\left(x_{t+1}\right)\right] \
& =E\left(r_t\right)+\gamma V\left(x_{t+1}\right)
\end{aligned}

+ 老样子这还是一个回归任务，用均方差损失，$E\left(r_t\right)$ 用采样来近似， + $\mathcal{L}=\frac{1}{2}\left(E\left(r_t\right)+\gamma V\left(x_{t+1}\right)-V\left(x_t\right)\right)^2 \approx \frac{1}{2}\left(r_t+\gamma V\left(x_{t+1}\right)-V\left(x_t\right)\right)^2$ + 这种将一次采样所有再进行拟合的训练方式，转化为采样一步＋函数下一步的值来近似的方法：$G\left(x_t\right) \rightarrow r_t+V\left(x_{t+1}\right)$ ，就叫做时序差分法（Temporal Difference）。#card + 本质上来说这种方法存在的意义就是为了降低随机性，也就是降低方差。 + 当 $V\left(x_t\right)$ 是 $E\left[G\left(x_t\right)\right]$ 的无偏估计时，TD法也是蒙特卡洛法的无偏估计。 + 但是事实上 $V\left(x_t\right)$ 做不到无偏估计 $E\left[G\left(x_t\right)\right]$ ，所以TD法也是有偏的。 ## 优势/动作价值函数/状态价值函数 + 策略函数的loss $\mathcal{L}=\sum_{t=1}^T\left[G\left(x_t\right)-V\left(x_t\right)\right] \log P\left(x_t \mid x_{<t}\right)$ + 同样的动机(降低方差)，同样的形式，我们也用TD法改造一下：#card + $\mathcal{L}=\sum_{t=1}^T\left[r_t+\gamma V\left(x_{t+1}\right)-V\left(x_t\right)\right] \log P\left(x_t \mid x_{<t}\right)$ + $\mathcal{L}=\sum_{t=1}^T\left[r_t+\gamma V\left(x_{t+1}\right)-V\left(x_t\right)\right] \log P\left(x_t \mid x_{<t}\right)$ 到 $\mathcal{L}=\sum_{t=1}^T A\left(x_t\right) \log P\left(x_t \mid x_{<t}\right)$ + 这里面的 V 我们已经说过了，它叫状态价值函数，表达的是 :-> 没有采样 $x_t$ 时句子的回报。 + 我们记：$Q\left(x_t\right)=r_t+\gamma V\left(x_{t+1}\right)$ ，称为动作价值函数，表示 :-> 执行了＂采样 $x_t$＂这个动作后句子的回报。 + 记：$A\left(x_t\right)=Q\left(x_t\right)-V\left(x_t\right)$ ，称为优势，表示 :-> ＂采样 $x_t$＂这个动作相比于没有采样时的优势。 ## [[GAE]] + 表示时序差分 $\mathrm{T}-\mathrm{t}+1$ 步的近似，也就相当于完全通过采样来近似，就等于 $G\left(x_t\right)$ #card + 看到我们的动作价值函数： +

Q\left(x_t\right)=r_t+\gamma V\left(x_{t+1}\right)

$$+ 将这个函数记为： +$$

T D(1)=Q\left(x_t\right)=r_t+\gamma V\left(x_{t+1}\right)

+ 表示时序差分一步对 $G\left(x_t\right)$ 的近似，那么TD（2）： +

T D(2)=r_t+\gamma r_{t+1}+\gamma^2 V\left(x_{t+2}\right)

$$+ 表示时序差分 2 步的近似，以此类推TD（T－t＋1）： +$$

\begin{aligned}
T D(T-t+1) & =r_t+\gamma r_{t+1}+\ldots+\gamma^{T-t} r_T \
& =G\left(x_t\right)
\end{aligned}

+ 之前我们提到过，$T D(1)$ 是有偏的，偏差来自于 V 的偏差，但是它的随机变量少，方差低。随着TD函数的递增，采样越来越多，方差越来越大，但是 V 的占比越来越小，偏差越来越小，直到彻底变为 $G\left(x_t\right)$ 。两种方法各有各的好，对于这种＂多个方法各有各的好＂的情况，一个常见的做法是找 n 个和为 1 的系数，乘在每个方法上求加权和。看下面这种加权法：#card + $(1-\lambda) \sum_{n=1}^{\infty} \lambda^{n-1} T D(n)=(1-\lambda) T D(1)+(1-\lambda) \lambda T D(2)+\ldots +(1-\lambda) \lambda^{\infty} T D(\infty)$ + 首先把系数拿出来是一个几何级数 $(1-\lambda) \sum_{i=0}^{\infty} \lambda^i$ ，在 $\lambda<1$ 时收敛，系数和确实为 1。 + 再看每一项，当 $\lambda$ 越趋近于 0 时，$T D(0)$ 的占比越大，当 $\lambda$ 趋近于 1 时，$T D(\infty)$ 的占比越大。通过调控 $\lambda$ ，可以控制是用方差更小的时序差分法，还是偏差更小的蒙塔卡罗法。将这种＂我全都要＂方法带入优势的计算公式，就是广义优势估计： +

\hat{A}\left(x_t\right)=\left[(1-\lambda) \sum_{n=1}^{T-t} \lambda^{n-1} T D(n)\right]-V\left(x_t\right)

+ 这种写法是为了方便理解广义优势估计是如何平衡TD法和蒙特卡洛法的，实际使用的时候，下面这个公式更方便计算：#card +

\delta_t=r_t+\gamma V\left(x_{t+1}\right)-V\left(x_t\right)

$$+$$

\hat{A}\left(x_t\right)=\sum_{l=0}^{\infty}(\gamma \lambda)^l \delta_{t+l}

+ 引入GAE后策略模型的loss函数为：#card + $\mathcal{L}=\sum_{t=1}^T \hat{A}\left(x_t\right) \log P\left(x_t \mid x_{<t}\right)$ ## [\[\[重要性采样\]\]](/post/logseq/Importance%20Sampling.html) + 当有两个支撑集相同但概率密度不同的分布A、B时，可以在其中一个分布上采样，并利用修正系数，计算出另一个分布上的期望。 + 在训练的过程中为什么会存在两个有差异的分布？#card + 这就要从训练的方法上说起。在实际训练过程中，我们会先 根据rollout batch size采样出一批QA数据，然后再以 train batch size从这些QA中采样数据进行训练。这个 rollout batch size一般会大于 train batch size，也就是说train一个batch后，模型的参数更新了，但是rollout的数据还没训完，还得接着训。 + 这个时候rollout出来的数据是train这一个batch之前的模型采样出来的，这就导致采样模型和训练模型出现了偏差。rollout之所以会大于train是为了增大推理时的吞吐，提高推理效率。 + 但是这个推理过程其实可以被cover掉，比如我最近写的框架就将infer和train重叠了。 + 现在最新的vllm支持了sleep，且megatron和vllm的模型切分方式是相同的，理想情况是megatron将优化器卸载，通过共享内存将参数传递给vllm进程，原地转为vllm推理，然后vllm再sleep原地转megatron训练，性能更高。 + 所以rollout batch size现在也不是非要大于train。另一个可能的差异来源是一次rollout训多个epoch，这个就没办法了。 ## CLIP + 这个截断目的不是真的要把修正系数限制在某一个范围，而是要抛弃修正系数上下溢的数据不进行训练。 #card + 首先假设 $A$ 为正数，如果修正系数上溢，则被截断为 $1+\epsilon$ ，此时截断项比未截断项更小，会被min函数选中。如果下溢，截断项大于未截断项，截断项不会被选中。 + 截断后是没有梯度回传的，所以截断项被选中意味着这条数据被抛弃了。 + 理解一下：当A为正数，意味着应该增大 $x_t$ 的概率。如果此时发生上溢，则表示相比于采样模型，策略模型对 $x_t$ 的概率增加的已经很多了，不要再增加了。 + 如果下溢表示增加的还不够多，还可以继续增加。 + 如果 $A$ 为负数，逻辑也正好反过来。 ## Reference + 开头提到了KL散度，但是我们还没提PPO是怎么用的。之前还埋了一个伏笔，我们说把给整个句子打分的reward升级成了给每个token打分的reward，也没说是怎么升级的。其实在PRM之前没人升级这个，reward还是只给最后一个token打分，其他token的分数其实是用KL散度打的：#card + $r_t=\beta\left(K L\left(P_{\text {policy }} \mid P_{\text {reference }}\right)\right)=-\beta \log \frac{P_{\text {policy }}\left(x_t\right)}{P_{\text {reference }}\left(x_t\right)}$ + $\beta$ 是一个0－1之间的系数，当策略模型的概率高于reference，则r为负降低概率，反之则增加概率。也就是说这里KL散度是被乘在概率上了。当然另一种做法就是像GRPO那样，直接在策略loss之外单独加一个KLloss，这也是KL loss常见的用法。这两种方法的差异我感觉理解的还是太透彻，希望有其他大佬能够解惑。 + 另外这里还涉及一个小细节，就是critic模型在训练的时候，可以选择拟合这个算了 kl 的 reward，也可以拟合没有加上kl的reward，我倾向于不算。 ## 评论区 + 从您这学习到很多，有一个问题想要请教一下。对于GRPO这种将KL项提出来的，那么同一个response的每个token的Advantage是不是都一样了呢，是不是就是您所说的加权语言损失。。。 谢谢！ #card + 不一样，是语言模型loss有两个要求，一个是sentence粒度权重，一个是权重非负，grpo不满足权重非负。 引入kl确实可以视为一种token粒度的奖励，但是这个奖励意义到底是什么，是否真的需要是需要讨论的。事实上我们现在一般不怎么加kl了，加kl权重也很小，千分之一万分之一这种。 + 突然发现引入kl本身是不是就会对不同token带来不同影响呀，不知道我的理解对不对 + 想请教老师一个问题，GRPO对比RF++，前者是在一个问题内采样的多个轨迹上算baseline，后者我不是很清楚，它是相当于有一个batch size=n的问题，每个问题采样一个(?)轨迹，然后n个问题-轨迹得到的reward计算baseline吗？#card + grpo和reinforce++的本质区别应该是是group norm vs batch norm。至于kl放在哪里，每个prompt是采样一个response还是多个都是可调超参。 + 此刻起优化目标彻底脱离“最大化数据的对数似然”，变为“最大化奖励的期望” `` 这句话该怎么理解呢？#card + 只要模型还是在最大化对数似然，就还是语言模型，loss本身不会导致模型说不出人话。对于模型的优化，还是以数据正确性为主而不是训练稳定性。 在变为最大化奖励之后，模型的唯一目标就是追求高奖励，可以用不说人话、hack等等一切方式提高奖励。这个时候就要开始考虑训练稳定性了。 + 但实践中碍于各种因素影响，也不是说最大化对数似然就一定不会崩，比如on-policy的rejection sampling，模型依旧可能崩。这个原因比较复杂，我打算下一篇实验篇再展开。 +