DCMT 模型

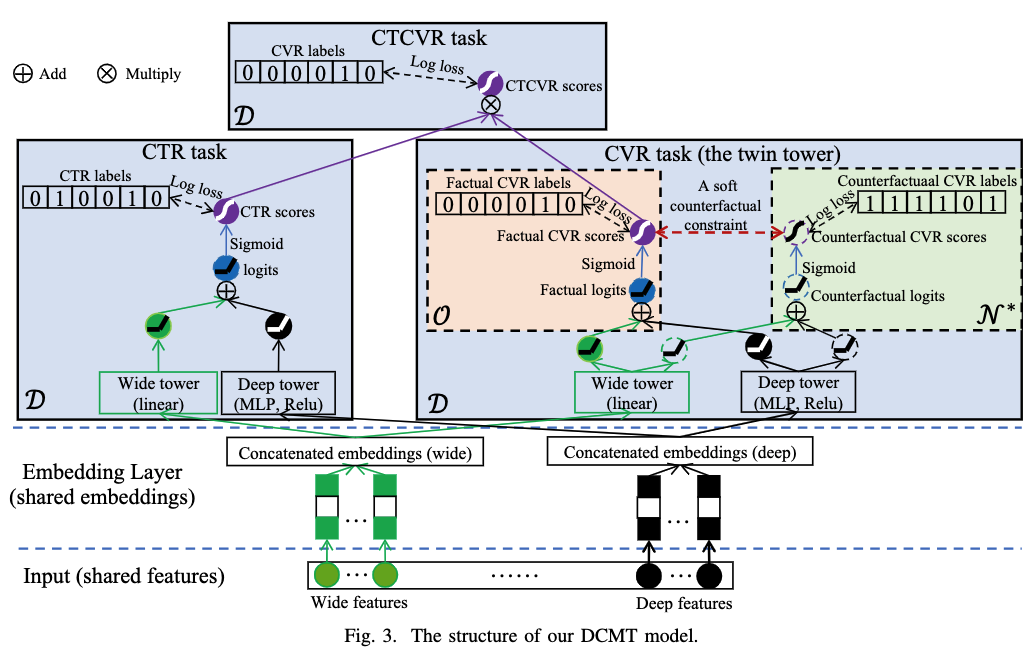
• 整体的目标公式是 :-> $L(\theta)=\mathcal{E}^{\mathrm{CTR}}+w^{c v r} \mathcal{E}^{\mathrm{DCMT}}+w^{c t c v r} \mathcal{E}^{\mathrm{CTCVR}}+\lambda_2|\theta|_F^2$
• 特征划分成wide和deep两部分，分别得到对应的wide embedding和deep embedding

主任务CVR task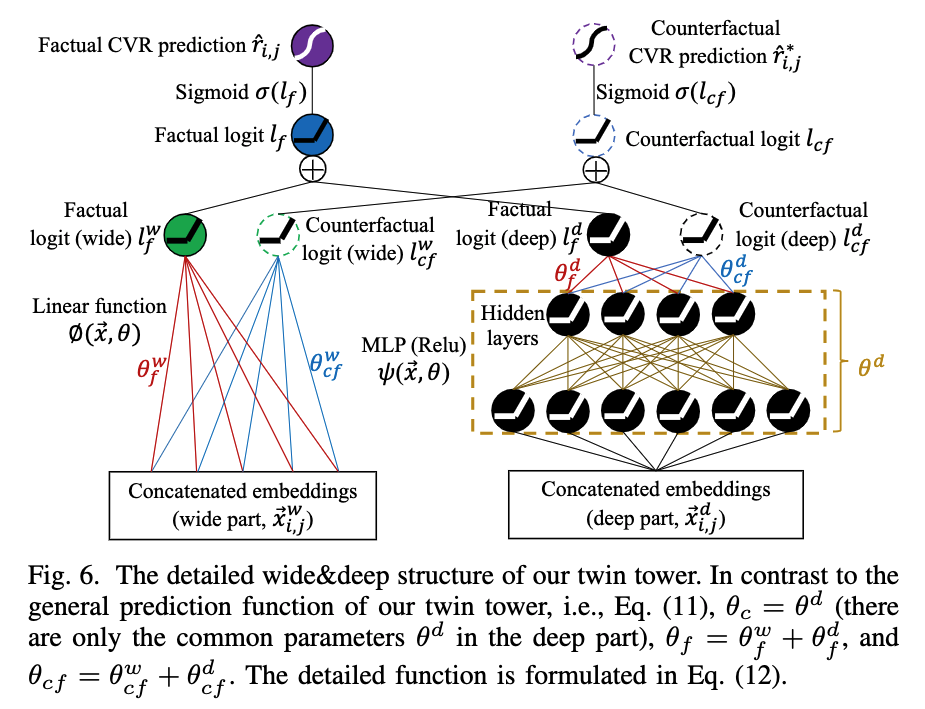

• #card 事实转化率 + 反事实转化率公式：$\left\langle\hat{r}{i, j}, \hat{r}{i, j}^*\right\rangle=\left\langle\sigma\left(l_f\right), \sigma\left(l_{c f}\right)\right\rangle$

  • $$
    \begin{gathered}
    =<\sigma\left(l_f^w+l_f^d\right), \sigma\left(l_{c f}^w+l_{c f}^d\right)> \
    =<\sigma\left(\phi\left(\vec{x}_{i, j}^w ; \theta_f^w\right)+\psi\left(\vec{x}_{i, j}^d ; \theta^d, \theta_f^d\right)\right), \sigma\left(\phi\left(\vec{x}_{i, j}^w ; \theta_{c f}^w\right)+\psi\left(\vec{x}_{i, j}^d ; \theta^d, \theta_{c f}^d\right)\right)>
    \end{gathered}
    $$

  • 这里的 $\sigma()$ 是Sigmoid函数，$\phi(\vec{x}, \theta)$ 是线性回归函数，$\psi(\vec{x}, \theta)$ 则对应的MLP结构。具体的 $\theta$ 已经在图中标清楚了。除了根据wide embedding $\vec{x}{i, j}^w$ 和deep embedding $\vec{x}{i, j}^d$ 分别用线性和深度结构来处理，这其实就是一个双子塔结构。这个双子塔的输入是一样的，即 $\vec{x}{i, j}^w+\vec{x}{i, j}^d$ ，但是输出则是两个，分别对应事实CVR（factual CVR）$\hat{r}{i, j}$ 和反事实CVR （counterfactual CVR）$\hat{r}{i, j}^$ 。

  • 这样的双子结构其实可以很好地模拟用户做转化决策的过程。面对同样的输入特征 $x_{i, j}$ ，样本有一定的概率 $\hat{r}{i, j}$ 进入事实空间，有一定概率 $\hat{r}{i, j}^$ 进入反事实样本空间。而我们模型中，加入了一个软性约束（先验知识） $\hat{r}{i, j}+\hat{r}{i, j}^ \approx 1$ 来控制这两个CVR的预测值。