Skip-Gram

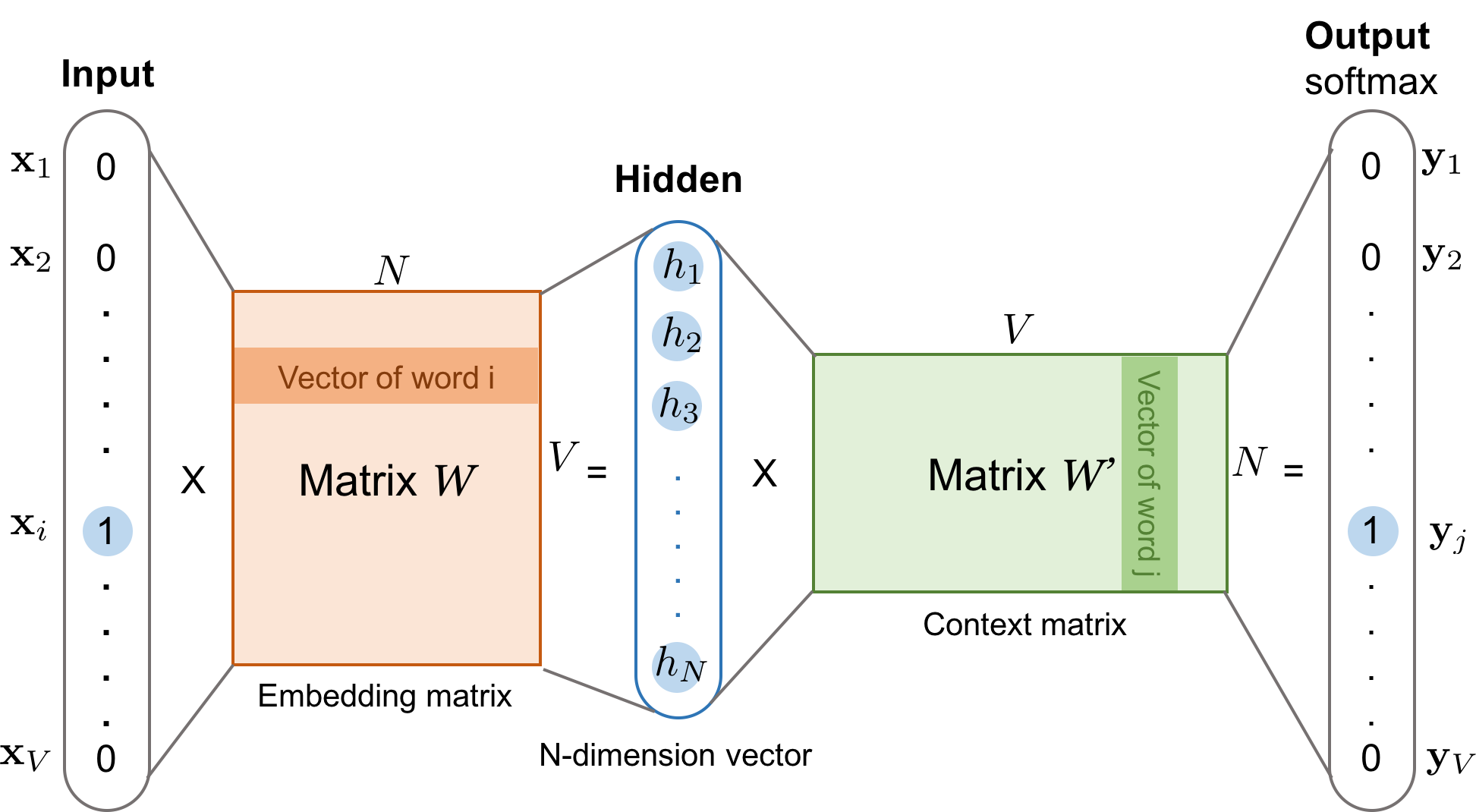
目标：网络的多个输出之间的条件概率最大。

C 个输出概率分布相同，并且得分最高的单词不是一定是预测单词。

假设第 c 个输出的第 j 个分量为 $${u^c_j=w_j h_{u_j}^c}$$

$${y_j^c=p(word^c_j|\vec X)=\frac{exp(u^c_j)}{\sum^V_{k=1}exp(u^c_k)}}$$

$${y^c_j}$$表示第 c 个输出中，词汇表 V 中第 j 个单词 $${word_j}$$ 为真实输出单词的概率。

损失函数定义

$$E = -\log \prod_{c=1}^{C} \frac{\exp \left(u_{j_{e}}^{c}\right)}{\sum_{k=1}^{V} \exp \left(u_{k}^{c}\right)}$$

$${j^*_c}$$ 为输出单词序列对应于词典 V 中的下标序列。

每个网络的输出相同，化简得到：

$$E=-\sum_{c=1}^{C} u_{j_{c}^{*}}^{c}+C \log \sum_{k=1}^{V} \exp \left(u_{k}\right)$$

^^隐层的激活函数其实是线性的？^^

skip gram 样本进行抽样：词频高的词(the)会在样本中大量出现，远远超过需要的训练样本数。

• （三）通俗易懂理解——Skip-gram的负采样 - 知乎

• 基本思想：对于我们在训练原始文本中遇到的每一个单词，它们都有一定概率被我们从文本中删掉，而这个被删除的概率与单词的频率有关。

• 保留某个单词的概率 $$P\left(w_{i}\right)=\left(\sqrt{\frac{Z\left(w_{i}\right)}{0.001}}+1\right) \times \frac{0.001}{Z\left(w_{i}\right)}$$

  • Z wi 在语料中的词频

  • 0.001 越大代表有越大的概率被我们删除

  • threshold for configuring which higher-frequency words are randomly downsampled

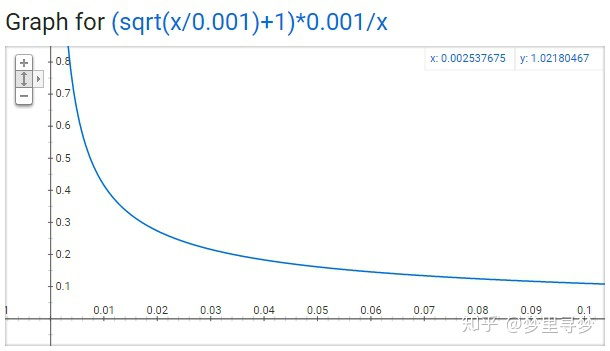
+ x 代表 z，y 代表 p

  + z 小于 0.0026 100%保留

  + z = 0.00746 50%bclq