张量积

任意两个大小矩阵之间的运算

$A \otimes B$

$\boldsymbol{a} \otimes \boldsymbol{b}=\left[\begin{array}{c}a_{1} \ a_{2} \ \vdots \ a_{n}\end{array}\right]{n \times 1} \otimes\left[\begin{array}{c}b{1} \ b_{2} \ \vdots \ b_{m}\end{array}\right]{m \times 1}=\boldsymbol{a} \boldsymbol{b}^{\mathrm{T}}=\left[\begin{array}{c}a{1} \ a_{2} \ \vdots \ a_{n}\end{array}\right]\left[\begin{array}{c}b_{1} \ b_{2} \ \vdots \ b_{m}\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{cccc}a_{1} b_{1} & a_{1} b_{2} & \cdots & a_{1} b_{m} \ a_{2} b_{1} & a_{2} b_{2} & \cdots & a_{2} b_{m} \ \vdots & \vdots & \ddots & \vdots \ a_{n} b_{1} & a_{n} b_{2} & \cdots & a_{n} b_{m}\end{array}\right]_{n \times m}$

$\boldsymbol{A} \otimes \boldsymbol{B}=\left[\begin{array}{ll}a_{1,1} & a_{1,2} \ a_{2,1} & a_{2,2}\end{array}\right] \otimes\left[\begin{array}{ll}b_{1,1} & b_{1,2} \ b_{2,1} & b_{2,2}\end{array}\right]=\left[\begin{array}{ll}a_{1,1} \boldsymbol{B} & a_{1,2} \boldsymbol{B} \ a_{2,1} \boldsymbol{B} & a_{2,2} \boldsymbol{B}\end{array}\right]$

几何解释

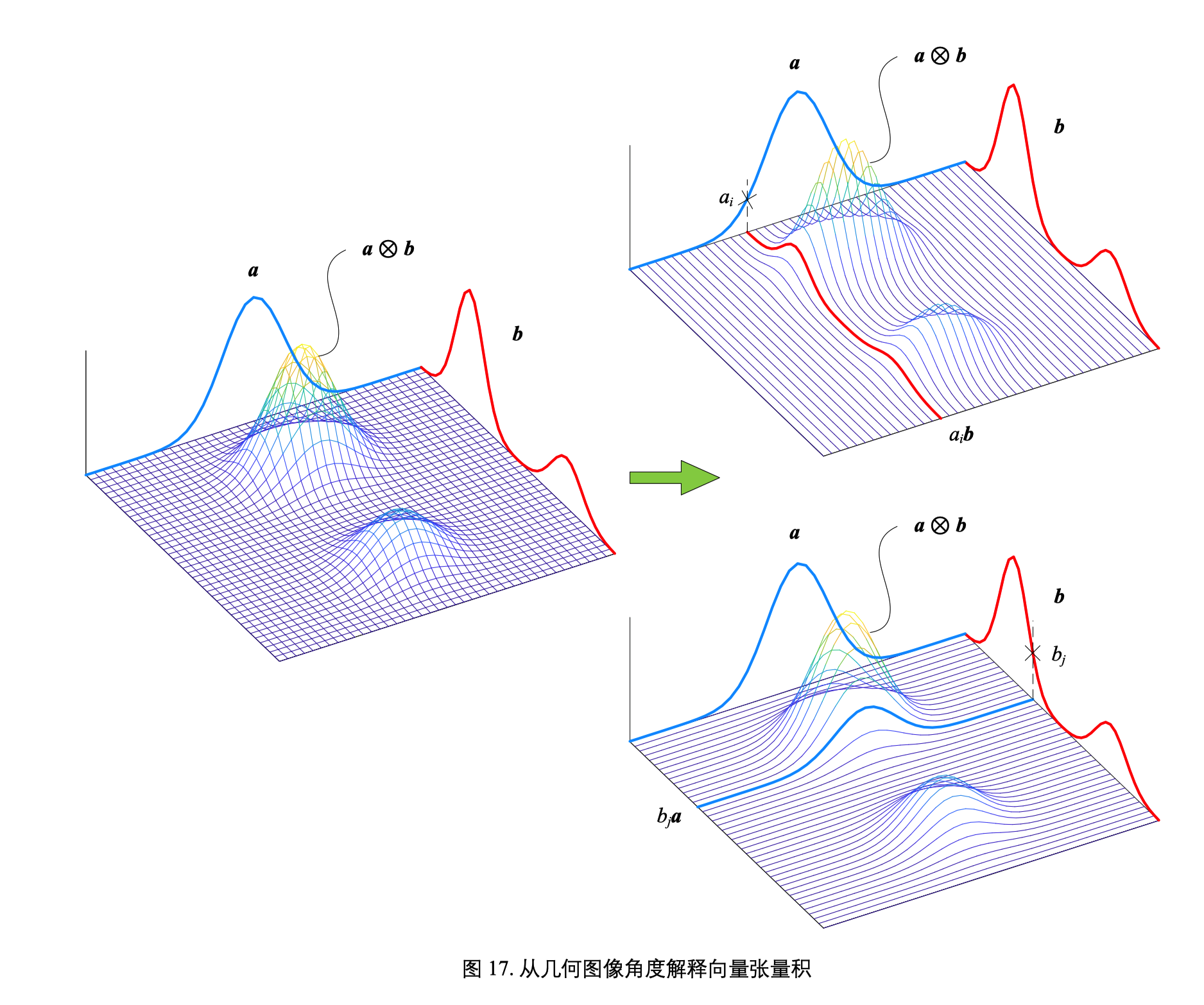
离散随机变量独立条件下，联合概率 pxy 是 px 和 py 的边缘概率的乘积 [[从加减乘除到机器学习/矩阵力量]] ch02