范数

范数是一种用来度量某个向量空间中的向量长度或大小的手段。

P范数

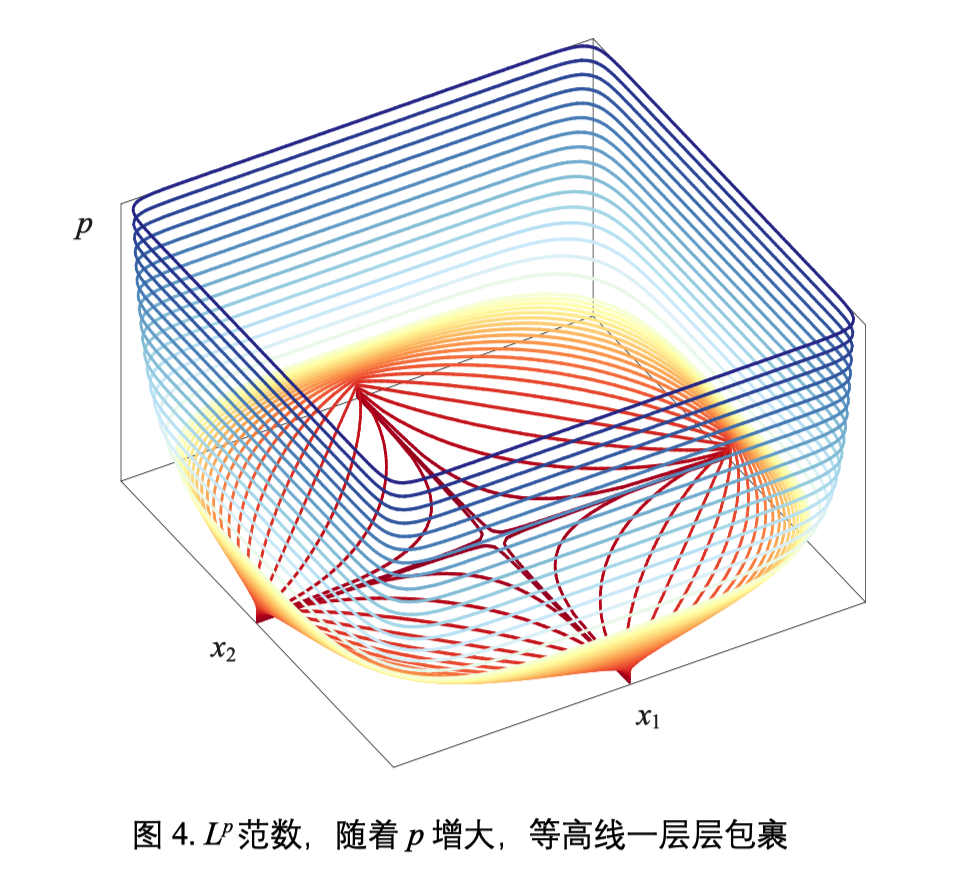
• $\|\boldsymbol{x}\|_{p}=\left(\left|x_{1}\right|^{p}+\left|x_{2}\right|^{p}+\cdots+\left|x_{D}\right|^{p}\right)^{1 / p}=\left(\sum_{i=1}^{D}\left|x_{i}\right|^{p}\right)^{1 / p}$

• 考虑 f(x1,x2), p 越大，范数值的图形越接近正方形

+ 

凹凸形

• p>1 范数等高线形状为凸

• 0<p<1 范数等高线形状为凹

L1 范数

• 曼哈顿距离

• 套索回归 [[LASSO regression]]

L2 范数

• 欧几里得距离

• [[岭回归]]

[[弹性网络回归]] 不同比例引入 L1 和 L2 正则项

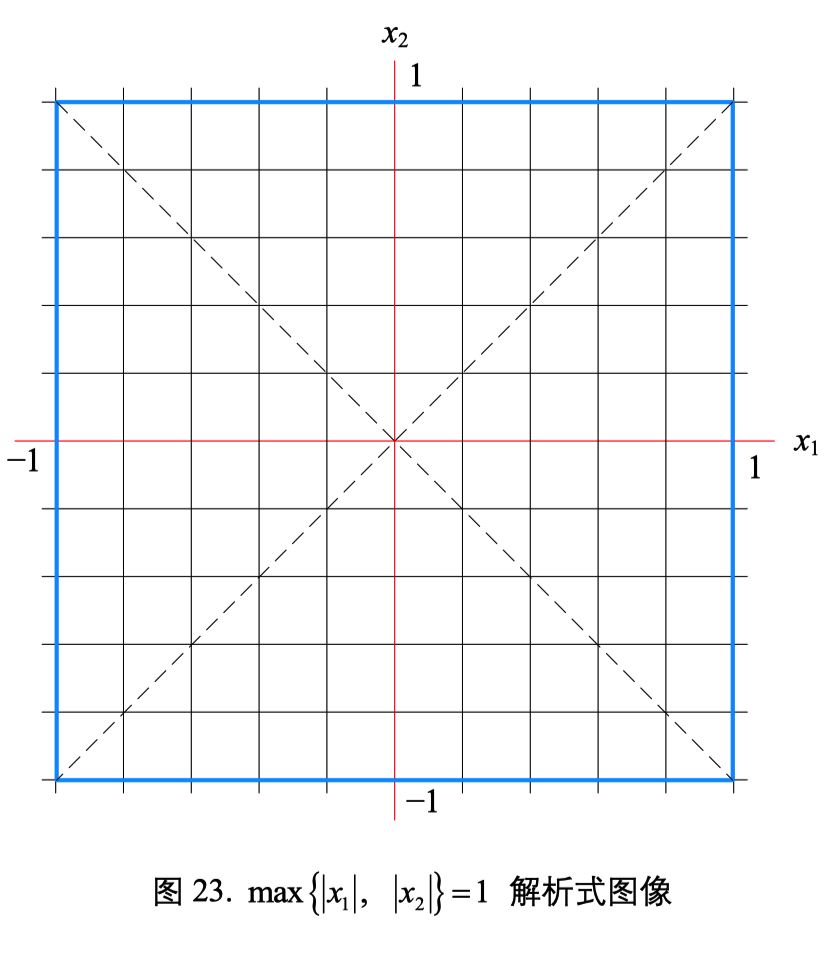
$L^{\infty}$ 范数：正方形

• 切比雪夫距离 Chebyshev distance

• $\|\boldsymbol{x}\|_{\infty}=\max \left(\left|x_{1}\right|,\left|x_{2}\right|, \cdots,\left|x_{D}\right|\right)$

• 几何图形

  • $\max \{\left|x_{1}\right|,\left|x_{2}\right| \}= 1$

    • $\begin{cases}x_{1}=\pm 1 & x_{1}^{2}-x_{2}^{2}>0 \\ x_{2}=\pm 1 & x_{1}^{2}-x_{2}^{2}<0\end{cases}$

  • $x_1^2 - x_2^2 > 0$

    • $x_1^2 - x_2^2 = 0$ 双曲线

+ 该范数对应的图形