随手记 13 分钟读完 (大约1890个字)

@Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting

核心贡献

  • Temporal Fusion Transformer 框架 #card

    • recurrent layers for local processing
      ls-type:: annotation
      hl-page:: 1
      hl-color:: yellow

    • interpretable self-attention layers for long-term dependencie

ls-type:: annotation
hl-page:: 1
hl-color:: yellow

+ specialized components to select relevant features

ls-type:: annotation
hl-page:: 1
hl-color:: yellow

+ a series of gating layers to suppress unnecessary components

ls-type:: annotation
hl-page:: 1
hl-color:: yellow

  • 模型可解释性 interpretable insights into temporal dynamics
    ls-type:: annotation
    hl-page:: 1
    hl-color:: yellow

#card
+ 区分全局重要特征 globally-important variables for the prediction problem
ls-type:: annotation
hl-page:: 3
hl-color:: yellow

+ 持久的时间模式 persistent temporal patterns

ls-type:: annotation
hl-page:: 3
hl-color:: yellow

+ 显著事件 significant events

ls-type:: annotation
hl-page:: 3
hl-color:: yellow

核心问题

  • #card [[Multi-horizon Forecasting]] 包含复杂的输入特征组合 contains a complex mix of inputs

ls-type:: annotation
hl-page:: 1
hl-color:: green

+ 静态变量

  + 与时间无关的静态变量 including static (i.e. time-invariant) covariates

ls-type:: annotation
hl-page:: 1
hl-color:: green

+ 时变变量 Time-dependent Inputs

  + 已知未来输入 known future inputs,

ls-type:: annotation
hl-page:: 1
hl-color:: green

    + 未来节假日信息

  + 外生时间序列 exogenous time series that are only observed in the past – without any prior information on how they interact with the target.

ls-type:: annotation
hl-page:: 1
hl-color:: green

    + 历史顾客流量 historical customer foot traffic

ls-type:: annotation
hl-page:: 2
hl-color:: green

+ 相关示意图

  + [:span]

ls-type:: annotation
hl-page:: 2
hl-color:: yellow

  • 使用 attention 机制增强 :-> 选择过去相关特征 used attention-based methods to enhance the selection of relevant time steps in the past
    ls-type:: annotation
    hl-page:: 2
    hl-color:: yellow

  • 之前基于 DNN 方法的缺陷 #card

    • 没有考虑不同类型输入特征 fail to consider the different types of inputs
      ls-type:: annotation
      hl-page:: 2
      hl-color:: blue

      • 万物皆时序 构建模型时，将所有的特征按 time step 直接 concat 在一起，所有变量全部扩展到所有的时间步，无论是静态、动态的变量都合并在一起送入模型。

    • 假定所有外生输入都已知与未来 assume that all exogenous inputs are known into the future

ls-type:: annotation
hl-page:: 2
hl-color:: blue

+ 忽略重要的静态协变量 neglect important static covariates

ls-type:: annotation
hl-page:: 2
hl-color:: blue

  + 通常处理方法是预测时和其他时间相关特征连接
  • 已有深度学习方法是黑箱，如何解释模型的预测结果？#card
    • do not shed light on how they use the full range of inputs present in practical scenarios
      ls-type:: annotation
      hl-page:: 1
      hl-color:: blue

相关工作

  • [[@A Multi-Horizon Quantile Recurrent Forecaster]] Multi-horizon Quantile Recurrent Forecaster MQRNN 结构，同时预测未来多个时间步的值

  • deep state space 状态空间模型，统计学，hybrid network，类似工作 [[ESRNN]] [[N-BEATS]]

  • [[Explainable AI]]

    • post-hoc methods 事后方法（因果方法），不考虑输入特征的时间顺序 do not consider the time ordering of input features

ls-type:: annotation
hl-page:: 3
hl-color:: blue

  + [[LIME]]

  + [\[\[SHAP\]\]](/post/logseq/%40A%20Unified%20Approach%20to%20Interpreting%20Model%20Predictions.html)

+ 基于 attention 的架构对语言或语音序列有很好的解释，但是很难适用于多维度预测  attention-based architectures are proposed with inherent interpretability for sequential data

ls-type:: annotation
hl-page:: 3
hl-color:: blue

解决方法

  • [[Multi-horizon Forecasting]]

    • prediction intervals [[区间预测]] #card

      • [[DeepAR]] 直接修改模型的输出，模型不拟合原始标签，而是拟合人工指定的分布，通过蒙特卡洛采样取平均得到最终的点预测。

    • 分位数回归 [[Quantile Regression]]，每一个 time step 输出 $10^{th}$ $50^{th}$ $90^{th}$ #card

      • 不同分位数下预测能够产生预测区间，通过区间大小反应预测结果的不确定性。某个点在不同分位数线性回归的预测结果很接近，则预测确定性搞。

      • Quantile Outputs

      • $\hat{y}i(q, t, \tau)=f_q\left(\tau, y{i, t-k: t}, \boldsymbol{z}{i, t-k: t}, \boldsymbol{x}{i, t-k: t+\tau}, \boldsymbol{s}_i\right)$

      • 设计 [[quantile loss]]

        • $\begin{gathered}\mathcal{L}(\Omega, \boldsymbol{W})=\sum_{y_t \in \Omega} \sum_{q \in \mathcal{Q}} \sum_{\tau=1}^{\tau_{\max }} \frac{Q L\left(y_t, \hat{y}(q, t-\tau, \tau), q\right)}{M \tau_{\max }} \end{gathered}$

          • $Q L(y, \hat{y}, q)=q(y-\hat{y}){+}+(1-q)(\hat{y}-y){+}$ #card

            • q 代表分位数

            • $()_+ = \max (0,)$

            • 假设拟合分位数 0.9

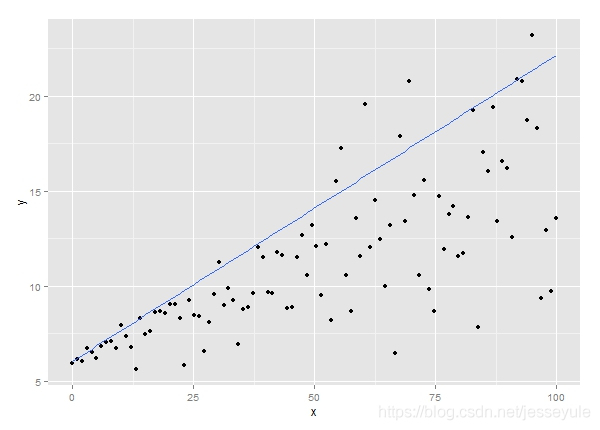
          + $Q L(y, \hat{y}, q=0.9)=\max (0.9 *(y-\hat{y}), 0.1 *(\hat{y}-y))$

          + $y-\hat{y} \gt 0$ 模型预测偏小，Loss 增加更多

          + loss 中权重 9:1，模型倾向预测出大的数字，Loss 下降快

        + 假设拟合分位数 0.5，退化成 MAE

          + $Q L(y, \hat{y}, q=0.5)=\max (0.5 *(y-\hat{y}), 0.5 *(\hat{y}-y)) = 0.5*|y-\hat{y}|$

+ q-Risk 避免不同预测点下的预测量纲不一致问题，对结果做正则化处理。目前只关注 P50 和 P90 两个分位数 #card
  + $q$-Risk $=\frac{2 \sum_{y_t \in \tilde{\Omega}} \sum_{\tau=1}^{\tau_{\max }} Q L\left(y_t, \hat{y}(q, t-\tau, \tau), q\right)}{\sum_{y_t \in \tilde{\Omega}} \sum_{\tau=1}^{\tau_{\max }}\left|y_t\right|}$

  • 模型结构
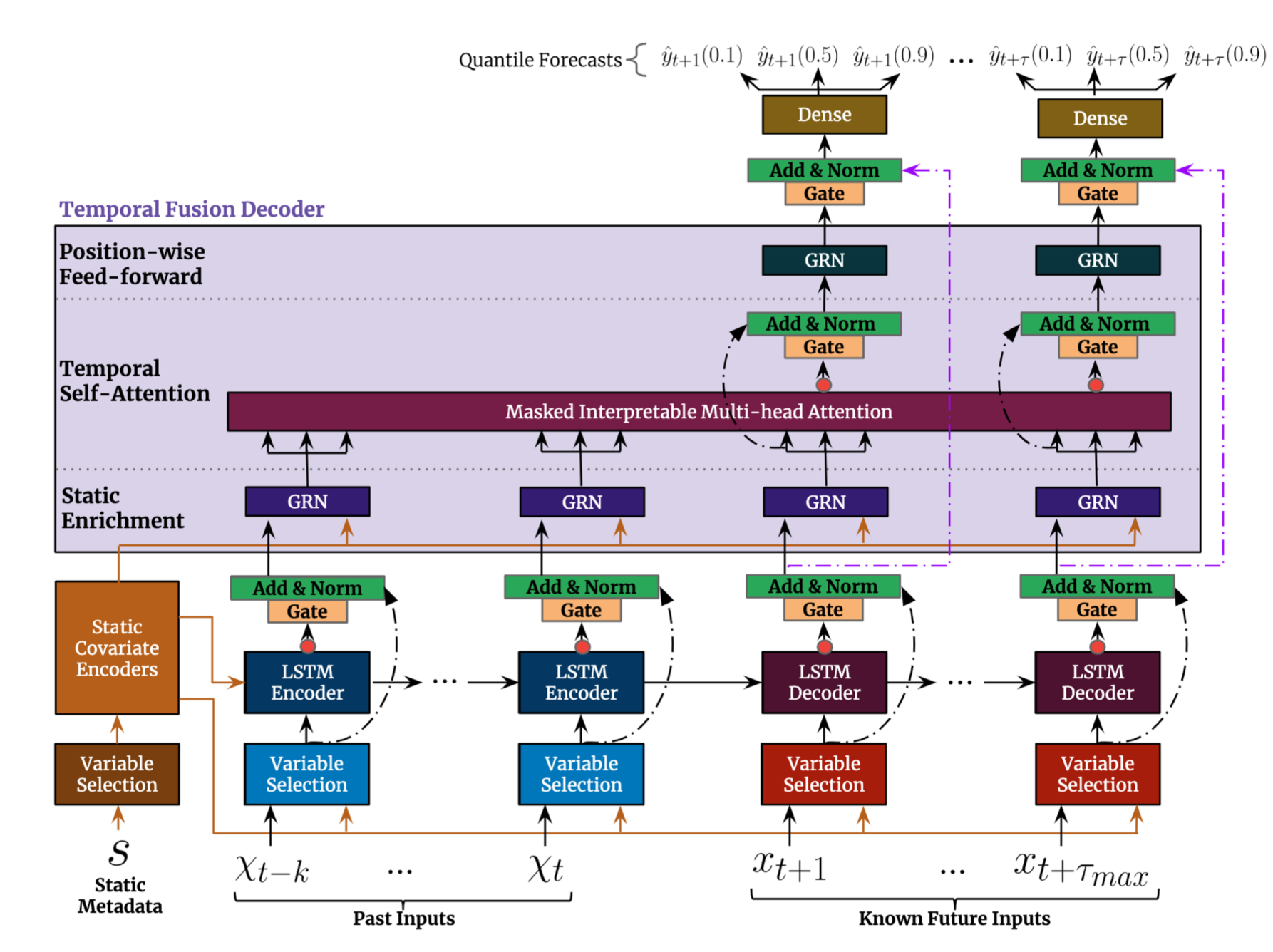
    image.png
    occlusion:: eyIuLi9hc3NldHMvaW1hZ2VfMTc1MDUxNDYxODQ4NV8wLnBuZyI6eyJjb25maWciOnsiaGlkZUFsbFRlc3RPbmUiOmZhbHNlfSwiZWxlbWVudHMiOlt7ImxlZnQiOjE2NS45NTY1MTg2NTE2NjgsInRvcCI6OTY5LjI2MTkzMjI3Mjc4NTEsIndpZHRoIjoxODcuODQ2NjE1ODY0ODQ1MiwiaGVpZ2h0IjozMTMuODMyNDU2NzU5NjQwMSwiYW5nbGUiOjAsImNJZCI6MX0seyJsZWZ0Ijo1NjguMDQyNDkzNzIxMzAxMiwidG9wIjoxMjU0LjQxNjI0MDY3Njc3NTUsIndpZHRoIjo1MDkuNzE3NzA4ODg2NDEzNDUsImhlaWdodCI6MTI5LjkwMzUwOTYzNDg3NDM1LCJhbmdsZSI6MCwiY0lkIjoyfSx7ImxlZnQiOjEzNDcuODg5NDc4MzE0MDk3NSwidG9wIjoxMjU0LjQwNTA5NDg3NjE1MTUsIndpZHRoIjo1OTUuNzc4OTU2NjI4MTk1MSwiaGVpZ2h0IjoxNDMuMjA0NjU0OTE5MjU0MzgsImFuZ2xlIjowLCJjSWQiOjN9LHsibGVmdCI6MTAwMS41ODg0MzMxODAwMzA1LCJ0b3AiOjk2OS42Mjc3NzcyNDY0NzQ3LCJ3aWR0aCI6MTM0MS42ODQ4NTk1OTAzMzI3LCJoZWlnaHQiOjMzOS43NDc2NDA1ODM1MTY2LCJhbmdsZSI6MCwiY0lkIjo0fSx7ImxlZnQiOjEzNTguODg5NDc4MzE0MDk3MiwidG9wIjozMjEuMzI0NDU2ODQ3NjYwNSwid2lkdGgiOjY0MC40MDg3MjI0OTU3MDAyLCJoZWlnaHQiOjM5Ny4yNzQ2NTEwMTc3MzEzNCwiYW5nbGUiOjAsImNJZCI6NX0seyJsZWZ0IjoxOTMuNjc1MTU1ODg2NzAwNzYsInRvcCI6NTQxLjc3NDYzODcyMDc3NTYsIndpZHRoIjoyMzkuMDE2OTY2NzgyNzg3NTMsImhlaWdodCI6NDM2LjAxODAxNTE1NDExMzEsImFuZ2xlIjowLCJjSWQiOjZ9XX19

    • [:span]
      ls-type:: annotation
      hl-page:: 6
      hl-color:: yellow

  • 输入部分

    • [[Static Covariate Encoders]] 通过 GRN 将静态特征编码变成 4 个不同向量

    • 动态特征 #card

      • post inputs

      • known future inputs

    • [[Variable Selection Networks]] 通过选择重要的特征，减少不必要的噪音输入，以提供模型性能。 #card

      • [[GLU]] 灵感来自 LSTM 的门控机制，sigmoid 取值范围 0-1

    • 对不同类型的输入变量应该区别对待 #card

      • 静态变量通过特殊的 [[Static Covariate Encoders]]，后续做为 encoder 和 decoder 的输入

      • 过去的动态时变变量+动态时不变变量进入 encoder 结构中（蓝色 variable seletcion）

      • 未来的动态时不变变量进入 decoder 结构中

    • seq2seq with teacher forcing 架构 #card

      • encoder 部分动态特征 embedding 和静态特征 embedding concat 在一起做为输入

        • 静态变量 + 动态时变变量

      • decoder

        • 静态变量 + 动态时不变变量

  • 模型组成

    • [[Gated Residual Network]] 模型能够灵活地仅在需要时应用非线性处理 #card

      • 外生输入和目标之间的确切关系通常是事先未知的，因此很难预见那些变量是相关的。

      • 很难确定非线性处理的程度该多大，并且可能存在更简单的模型就能满足需求。

    • [[Interpretable Multi-Head Attention]]

    • [[Temporal Fusion Decoder]] 学习数据集中的时间关系

    • 通过 dense 层得到多个 [[Quantile Outputs]] #card

      • $\hat{y}(q, t, \tau)=\boldsymbol{W}_q \tilde{\boldsymbol{\psi}}(t, \tau)+b_q$

[[TFT Interpretability Use Cases]] #card

  • 输入特征重要性 examining the importance of each input variable in prediction
    ls-type:: annotation
    hl-page:: 17
    hl-color:: yellow

  • 可视化当前时间模式 visualizing persistent temporal patterns
    ls-type:: annotation
    hl-page:: 17
    hl-color:: yellow

  • 识别导致任何导致时间动态显著变化的时间 identifying any regimes or events that lead to significant changes in temporal dynamics
    ls-type:: annotation
    hl-page:: 17
    hl-color:: yellow

[[Ref]]

 
关注我

分类

链接

最新文章

标签

LeetCode102
web68
Paper41
Algorithm39
weekly35
@麻将杰作“何切”300选27
Problems/202522
Article20
rk19
Workflow18
Mathematics16
Book14
Dynamic Programming13
life12
blog12
book11
implementation11
acm10
ReRank10
Problems10
×