ARIMA
适用情形:平稳的时间序列
平稳性和差分
[[平稳性]]:平稳的时间序列的性质不随观测时间变化而变化,具有 趋势性或季节性 的时间序列是非平稳的。
- 白噪声序列是平稳的,也是 随机不可 预测的。
- 平稳的时间序列的ACF会 快速下降到接近0 。
- [[单位根检测]]是一种常用的判断数据是否平稳的方法。
[[差分]] 计算了观测值之间的差值,衡量的是两者间的 变化/斜率 ,经过一次或多次差分后可以得到平稳的时间序列
- 在点预测时只需要进行 差分的逆运算 就行,分布预测的情况会更复杂一些。
一种常用的变换是对数变化,它可以用于平稳时间序列的方差,在时间图中方差可以理解为 上下波动 的程度。
[[延迟算子]] 表示时间序列的延迟,由于符合代数变换的规则,可以方便地表示 :-> 差分的组合。 - 一次运算 :-> $B y_t=y_{t-1}$
- 两次运算 :-> $\quad B\left(B y_t\right)=B^2 y_t=y_{t-2}$
- 一阶差分 :-> $\quad y_t^{\prime}=y_t-y_{t-1}=y_t-B y_t=(1-B) y_t$
- 二阶差分 :-> $\quad y_t^{\prime \prime}=y_t-2 y_{t-1}+y_{t-2}=\left(1-2 B+B^2\right) y_t=(1-B)^2 y_t$
- d 阶差分 :-> $(1-B)^d y_t$
- 季节差分>一阶差分 #card
- $$\begin{aligned}
(1-B)\left(1-B^m\right) y_t & =\left(1-B-B^m+B_i^{m+1}\right) \boldsymbol{y}t \
& =y_t-y{t-1}-y_{t-m}+y_{t-m-1}
\end{aligned}
$$
- $$\begin{aligned}
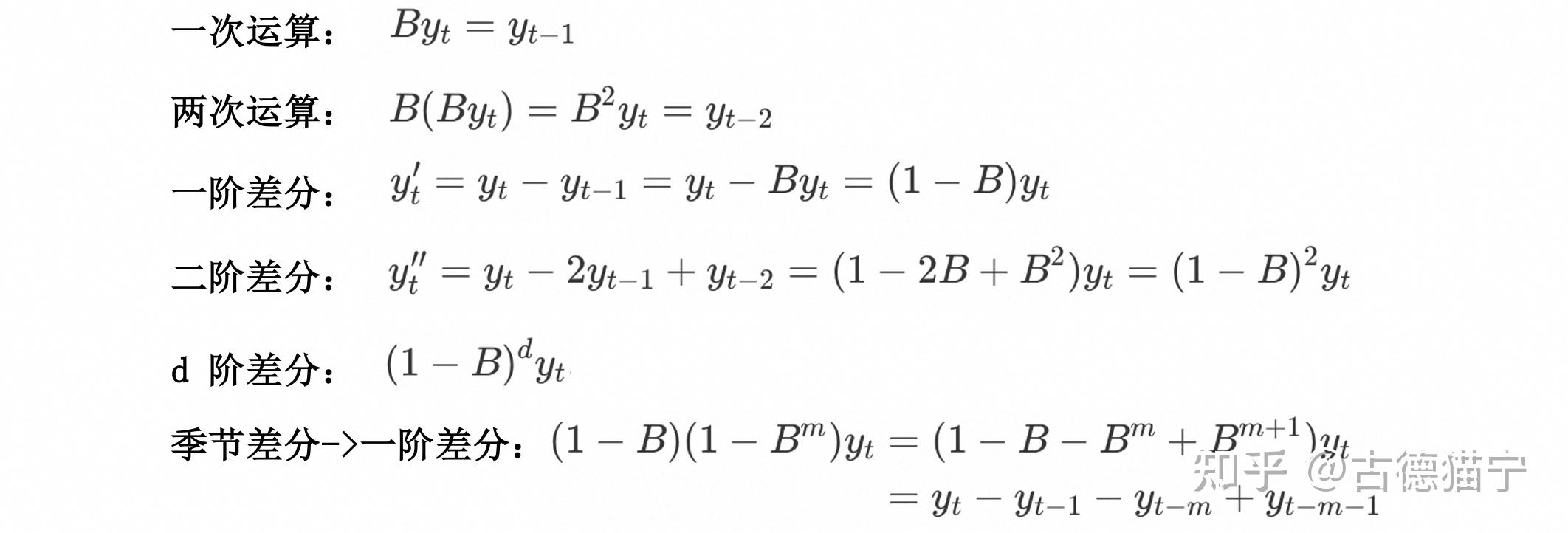
步骤 #card #incremental #depth-1
- 对序列进行 ADF 检验,观察序列是否平稳
- 对于非平稳的时间序列 :-> 要先进行 d 阶差分,转化为平稳时间序列
- 对平稳的时间序列分别求 ACF 和PACF,两个图求出最佳阶数 p、q #card
- 拖尾指序列以指数率单调递减或震荡衰减,而截尾指序列从某个时点变得非常小

+ 平衡预测误差与模型复杂度
+ AIC 准则全称是[[最小化信息量准则]](Akaike Information Criterion) #card
+ BIC(Bayesian InformationCriterion)[[贝叶斯信息准则]] #card
- 根据 p d q 得到模型,对模型的结果进行校验