Loss Function
MSE/MAE/ [[Huber Loss]]
假设误差服从某种特定分布,然后通过 MLE 推导最终 loss 形式。
MSE 反向传播梯度 $-\left(y^{(i)}-\theta^T x^{(i)}\right) x^{(i)}$
MSE 梯度容易受到异常值影响。异常样本 label 非常大时,$y^{(i)}-\theta^T x^{(i)}$ 的值也会非常大,将模型带偏。
- 反过来离群点会影响业务时,应该使用 MSE。
MAE 反向传播梯度 $-\frac{y^{(i)}-\theta^T x^{(i)}}{\left|y^{(i)}-\theta^T x^{(i)}\right|} x^{(i)}$
- 使用 MAE 损失时,梯度始终相同。在接近最小值的时候减少学习率。
MSE 和 MAE (L2 损失和 L1 损失)
- 平方差更容易求解,绝对误差对离群点更加鲁棒。
- pb 如果只预测一个值,最小化 MSE 倾向于均值,最小化 MAE 倾向于中位数。对于异常点,中位数比平均值更鲁棒。(简单可以证明)
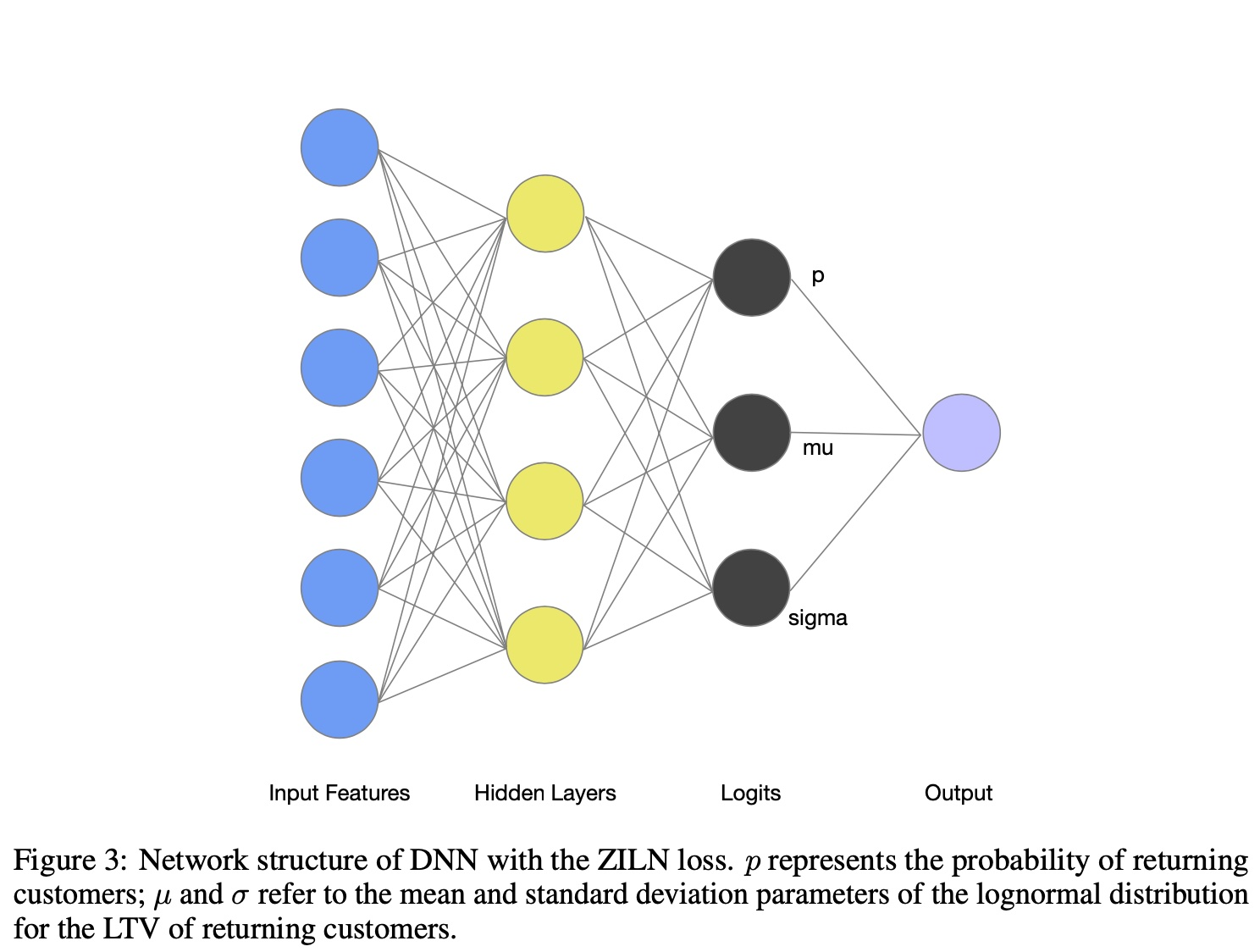
[[ZILN]] [[Log-Normal Distribution]]
- LTV 分布,首次购买后产生的价值,0 代表只购买一次

$L_{Z I L N}(x ; p, \mu, \sigma)=-\mathbf{1}{x=0} \log (1-p)-\mathbf{1}{x>0}\left(\log p-L_{\text {Lognormal }}(x ; \mu, \sigma)\right)$
x 是 label
p 预估购买概率
预估金额 $L_{\text {Lognormal }}(x ; \mu, \sigma)=\log (x \sigma \sqrt{2 \pi})+\frac{(\log x-\mu)^2}{2 \sigma^2}$
网络结构
[[Weighted Logistics Regression]] 预估用户观看时长
出处 [[@Deep Neural Networks for YouTube Recommendations]]
[[Cross Entropy Loss]] 正样本以时长为权重,负样本权重为 1。模型能学习到观看视频的时间
,reweight 后,改变正负样本的比例。- cross entropy 最终预估的概率是正样本的比例。
label 为 T 的样本,相当于在分类任务重变为 T 个正样本。正样本总体比例变成 $\frac{\sum_{i=1}^k T_i}{N+\sum_{i=1}^k T_i-k}$
- N 总样本,k 正样本,Ti 每个样本时长
LR 可以写成
$\frac{1}{1+e^{- \text {logit }}}=\frac{\sum_{i=1}^k T_i}{N+\sum_{i=1}^k T_i-k}=\frac{P}{N+P}$
$\frac{P}{N}=e^{\text {logit }}$
上面推导如果不忽略 k
label为 T 的样本,把它当做 T 个正样本和一个负样本,为每个正样本多增加一个负样本。
$\frac{1}{1+e^{-\operatorname{logit}}}=\frac{\sum_{i=1}^k T_i}{N+\sum_{i=1}^k T_i-k+k}$
reweight 之后相当于假设 label 服从参数为 p 的几何分布(失败概率),label T就是几何分布的 pdf 取 log 后提到前面的值,表示连续失败 T 次。
[[Bucketing with Softmax]] 对 label 的值域进行分桶,根据每个样本的 label 把样本分到某个桶里。回归任务转成多分类问题,使用 softmax 损失函数训练。
线上预测时,用 softmax 预估的概率分布对每个桶做加权求和。
- pred $=\sum_{i=1}^n p_i v_i$
如何确定分桶数量和每个桶大小?
- 目标让每个分桶的样本均衡
优化
- 每个桶再套上 mse 等损失转化成分区间的 multi-task 建模
分桶之后会丢失 laebl 之间的大小关系(label=50 分到 [0,10] 或 [51,100] 的损失没有区分性)。引入[[Label Smooth]]
- 对 label 做变换时,不用 one-hot 而是转化成高斯分布等形式
[[ETA]]
均值和中位数哪个大?均值大?
对于 badcase 来说,哪个模型效果更好?
MSE 对异常值更加
MAPE 没有上界,对异常值敏感,训练出来的模型倾向于低估。(高估带来较大的惩罚)
SMAPE 有界(0-200),高估和低估的上界都是 200 。