随手记 2 分钟读完 (大约356个字) 0次访问

Post Norm 和 Pre Norm 区别

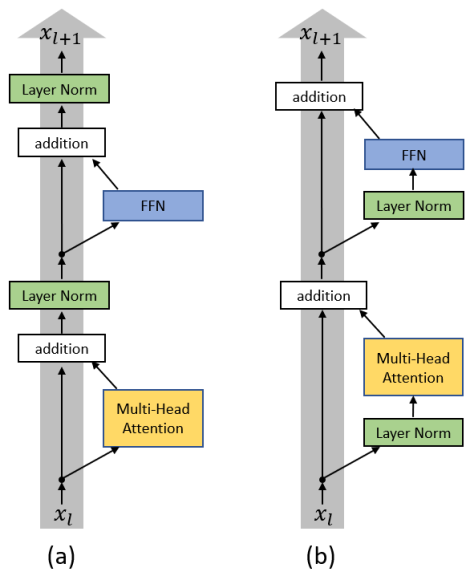
image.png

  • [[Pre Norm]] :<-> xn+1=xn+f(norm⁡(xn))x_{n+1}=x_{n}+f\left(\operatorname{norm}\left(x_{n}\right)\right)

    • 第二项的方差由于有 norm 不会随层数变化，x 的方差在主干上随层数累积。到达深层后，单层对主干的影响很小，不同层在统计上类似。

    • xn+2=xn+1+f(norm⁡(xn+1))=xn+f(norm⁡(xn))+f(norm⁡(xn+1))≈xn+2f(norm⁡(xn))x_{n+2}=x_{n+1}+f\left(\operatorname{norm}\left(x_{n+1}\right)\right)=x_{n}+f\left(\operatorname{norm}\left(x_{n}\right)\right)+f\left(\operatorname{norm}\left(x_{n+1}\right)\right) \approx x_{n}+2 f\left(\operatorname{norm}\left(x_{n}\right)\right)

    • 这样训练的深层模型更像是扩展模型宽度，相对好训练。

  • [[Post Norm]] :<-> xn+1=norm⁡(xn+f(xn))x_{n+1}=\operatorname{norm}\left(x_{n}+f\left(x_{n}\right)\right)

    • 主干方差恒定，每层对 x 都有较大影响，没有从头到尾的恒等路径，梯度难以控制，更难收敛，训练出来效果好。

    • 突出残差分支

    • [[BERT]]训练时，需要 warmup

      • 输出层的期望梯度非常大，不稳定
      • [[Adam]] 和 [[SGD]] 都需要

pre 和 post 具体含义 #card

  • 先 norm 再残差 [[Pre Norm]] :<-> xn+1=xn+f(norm⁡(xn))x_{n+1}=x_{n}+f\left(\operatorname{norm}\left(x_{n}\right)\right)

  • 先残差再 norm [[Post Norm]] :<-> xn+1=norm⁡(xn+f(xn))x_{n+1}=\operatorname{norm}\left(x_{n}+f\left(x_{n}\right)\right)

[[DeepNet]]

Ref

Post Norm 和 Pre Norm 区别

https://blog.xiang578.com/post/logseq/Post Norm 和 Pre Norm 区别.html

作者

Ryen Xiang

发布于

2024-10-05

更新于

2025-04-23

许可协议

 

相关文章

网络回响

评论

目录

关注我

最新文章

×