矩阵
方阵 symmetric matrix
对称矩阵 symmetric matrix
左下和右上元素以主对角线镜像对称
转置结果为本身
- $A=A^T$
[[对角矩阵]] diagonal matrix
副对角矩阵 anti-diagonal matrix
单位矩阵 identity matrix
- 对角线上元素是 1,其他元素是 0
三角矩阵 (triangular matrix)
- 如果矩阵 A 为可逆矩阵 (invertible matrix, non-singular matrix),A 可以通过 LU 分解变成一个下三角矩阵 L 与一个上三角矩阵 U 的乘积。
[[矩阵逆]]
$AB=BA=I$
逆 inverse $A^{-1}$
矩阵可逆也称为非奇异 non-singular
方阵
满秩
[[正交矩阵]] orthogonal matrix
行列式 determinant
将方阵A根据一定规则映射到一个标量
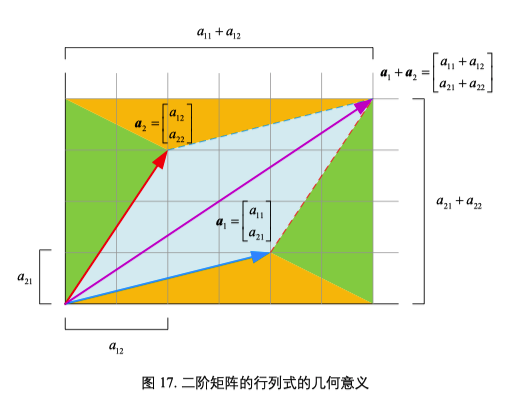
二阶矩阵行列式的几何意义
$\mathbf{A}=\left[\begin{array}{ll}a_{11} & a_{12} \ a_{21} & a_{22}\end{array}\right]$
行列式值是两个列向量构成的平行四边形面积
- 第一个向量顺时针到第二个向量的夹角小于 180 度结果为正
三阶矩阵行列式的几何意义
- 列向量构成平行六面体的体积
多维
多元高斯分布 $\varphi(x, \mu, \Sigma)=\frac{1}{(2 \pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}} e^{-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)}$
矩阵行列式 $|\Sigma|^{\frac{1}{2}}$,体积缩放
迹 trace
方阵主对角线之和
$\operatorname{tr}(\boldsymbol{A})=\sum_{i=1}^{n} a_{i, i}=a_{1,1}+a_{2,2}+\cdots+a_{n, n}$
矩阵乘向量:线性方程组
$Ax=b$
解的个数
欠定方程组 underdetermined system
超定方程组 overdetermined system
线性组合 linear combination
- $\left[\begin{array}{llll}a_{1} & a_{2} & \cdots & a_{D}\end{array}\right]{1 \times D}\left[\begin{array}{c}x{1} \ x_{2} \ \vdots \ x_{D}\end{array}\right]{D \times 1}=b{n \times 1}$
向量乘矩阵乘向量:二次型
quadratic form
$x^TQx=q$
- $\boldsymbol{x}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{x}=\sum_{i=1}^{D} q_{i, i} x_{i}^{2}+\sum_{i=1}^{D} \sum_{j=1}^{D} q_{i, j} x_{i} x_{j}=q$
二次曲线
- $f\left(x_{1}, x_{2}\right)=\left[\begin{array}{ll}x_{1} & x_{2}\end{array}\right]\left[\begin{array}{ll}a & b \ c & d\end{array}\right]\left[\begin{array}{l}x_{1} \ x_{2}\end{array}\right]=a x_{1}^{2}+(b+c) x_{1} x_{2}+d x_{2}^{2}$
方阵乘方阵 [[矩阵/分解]]
[[幂等矩阵]] idempotent matrix
$A^2=A$
[[对角矩阵]] :批量缩放
[[置换矩阵]] permutation matrix:调整元素顺序
由 0 和 1 组成的方阵,每一行每一列恰好有一个 1。
行向量左右翻转
- 行向量乘以副对角线上元素为1的方阵
长方阵
拉格姆矩阵 Gram matrix
$G=X^TX$
$\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right){i, j}=\boldsymbol{x}{i}^{\mathrm{T}} \boldsymbol{x}_{j}$
两两向量之间的相似度
[[协方差]]矩阵
元素平方和
- $\begin{aligned} \operatorname{trace}\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right) &=\operatorname{trace}\left[\begin{array}{cccc}\boldsymbol{x}{1} \cdot \boldsymbol{x}{1} & \boldsymbol{x}{1} \cdot \boldsymbol{x}{2} & \cdots & \boldsymbol{x}{1} \cdot \boldsymbol{x}{D} \ \boldsymbol{x}{2} \cdot \boldsymbol{x}{1} & \boldsymbol{x}{2} \cdot \boldsymbol{x}{2} & \cdots & \boldsymbol{x}{2} \cdot \boldsymbol{x}{D} \ \vdots & \vdots & \ddots & \vdots \ \boldsymbol{x}{D} \cdot \boldsymbol{x}{1} & \boldsymbol{x}{D} \cdot \boldsymbol{x}{2} & \cdots & \boldsymbol{x}{D} \cdot \boldsymbol{x}{D}\end{array}\right] \ &=\boldsymbol{x}{1} \cdot \boldsymbol{x}{1}+\boldsymbol{x}{2} \cdot \boldsymbol{x}{2}+\cdots+\boldsymbol{x}{D} \cdot \boldsymbol{x}{D} \ &=\sum_{i=1}^{n} x_{i, 1}^{2}+\sum_{i=1}^{n} x_{i, 2}^{2}+\cdots+\sum_{i=1}^{n} x_{i, D}^{2} \ &=\sum_{j=1}^{D} \sum_{i=1}^{n} x_{i, j}^{2} \end{aligned}$
张量积
[[爱因斯坦求和]] 约定
np.einsum('ij,jk->ik', A, B)
分块矩阵
+
列满秩
每一行都有非零的数
对应多个方程有解
[[正交投影]]