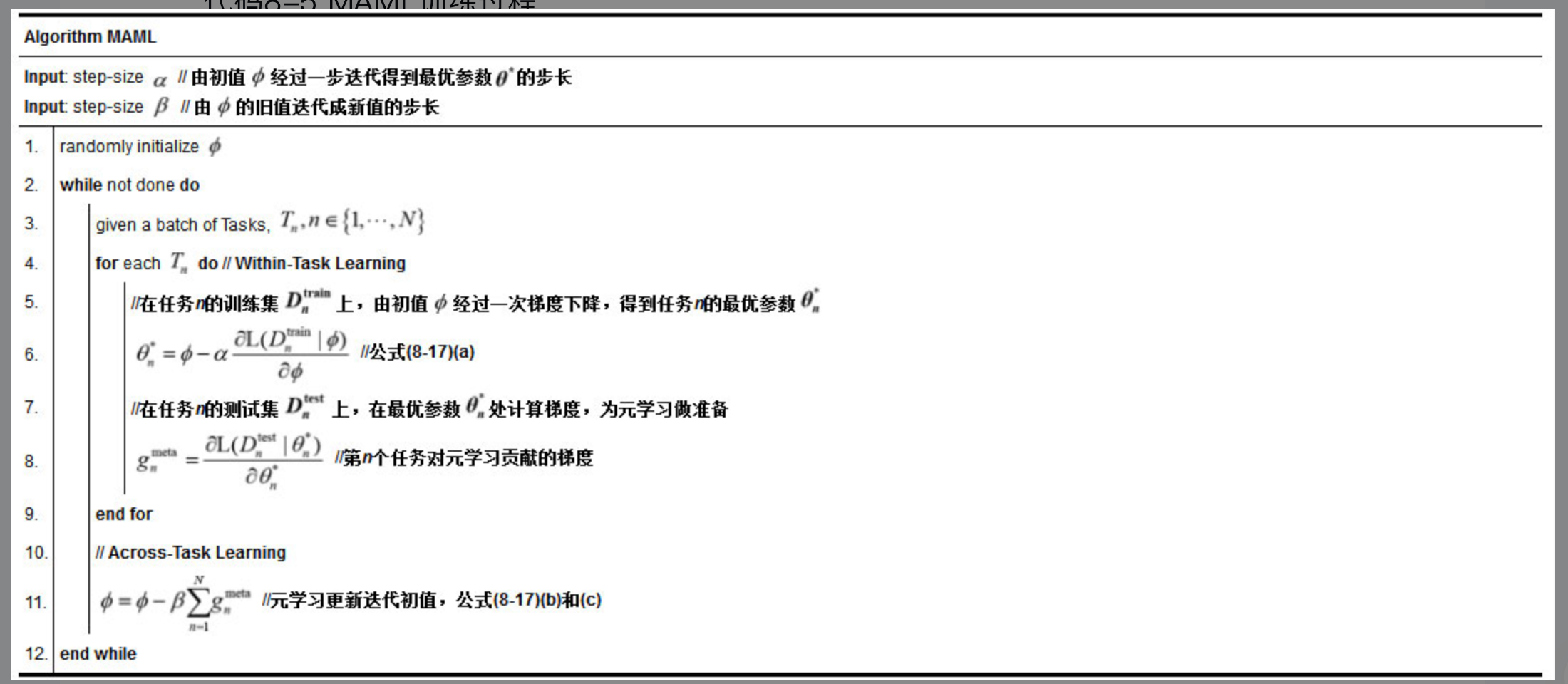
MAML

特点 #card

• 模板配置 $\phi$ 仅限于模型参数 $\theta$ 的初值；

• 损失函数 $L_{\text {meta }}(\phi)$ 对 $\phi$ 可导，从而可以通过SGD的方式求解出最优 $\phi$ ，也就是最优的 $\theta$ 初值。

提出MAML是为了解决小样本训练的问题，也就是新任务没有足够多的数据将模型参数从头训练好。MAML的解决思路是：#card

• 通过若干组任务（比如任务1是分类不同水果，任务2是分类不同的交通工具），学习出一套高质量的参数初值 $\phi$ ；

• 当面对一个新任务（比如分类不同动物时）时，由这段高质量的参数初值 $\phi$ 出发，只需要经过少量样本的迭代，就能得到适合新任务的最优参数 $\theta^*$ ，从而解决了新任务样本不足的问题。

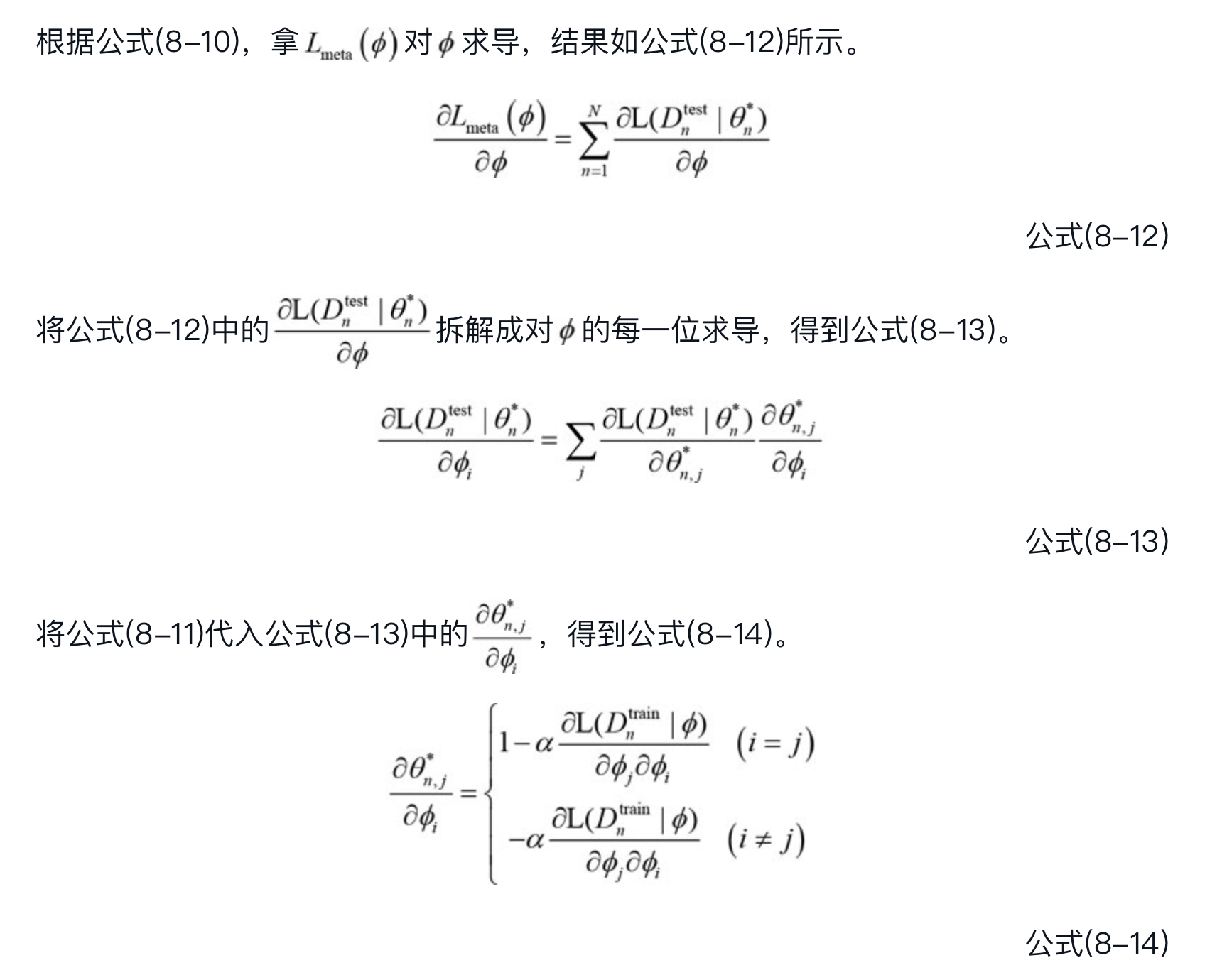
具体解法上，尽管理论上从初值 $\phi$ 出发，需要经过多轮训练迭代才能得到最优参数 $\theta^$ ，但是，从减少训练样本数的实际目标出发，我们假设初值 $\phi$ 只经过一次梯度下降就得到最优参数 $\theta^$：$\theta_n^*=\phi-\alpha \frac{\partial \mathrm{L}\left(D_n^{\operatorname{train}} \mid \phi\right)}{\partial \phi}$ #card

#card MAML 训练过程