NFM

$\hat{y}{N F M}(\mathbf{x})$ :-> $w{0}+\sum_{i=1}^{n} w_{i} x_{i}+f(\mathbf{x})$

• 第一项和第二项是线性回归

• 引入第三项神经网络学习 :-> 数据之间的高阶特征

  • 网络输入 :-> FM 模型的二阶特征交叉结果
  • 与直接使用高阶 FM 模型相比 :-> 可以降低模型的训练复杂度，加快训练速度。
    NFM 的神经网络部分包含 4 层，分别是 Embedding Layer、Bi-Interaction Layer、Hidden Layers、Prediction Score。

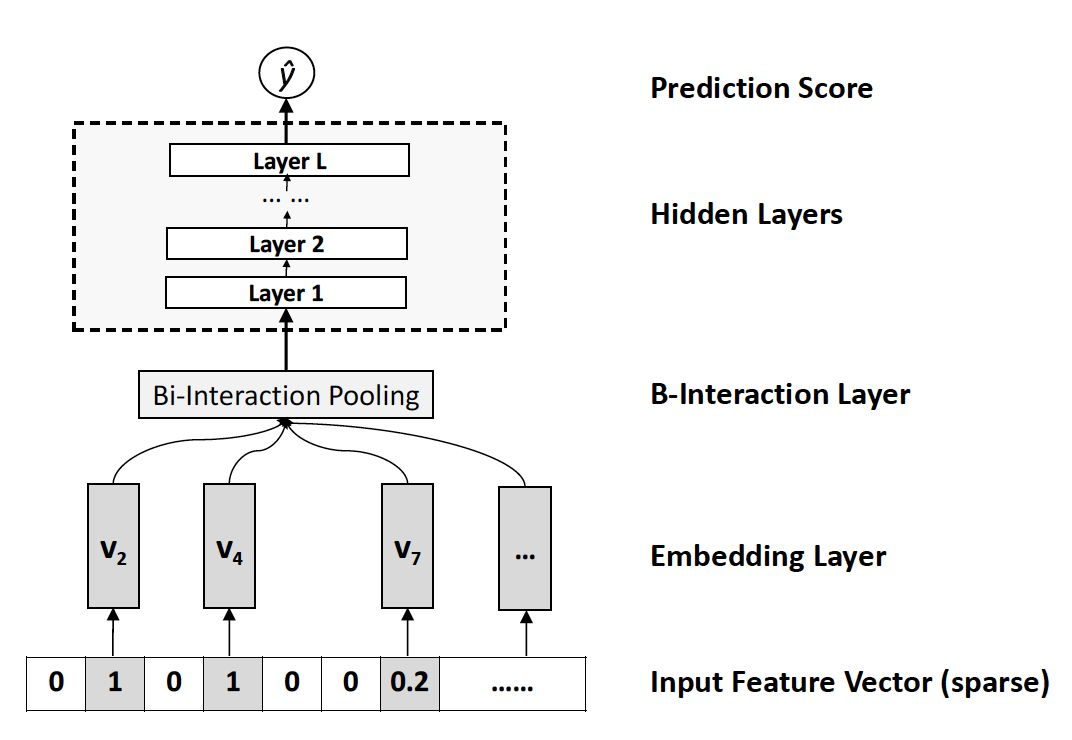
tags:: #[[Model Architecture]]

Embedding Layer 层对输入的稀疏数据进行 Embedding 操作。最常见的 Embedding 操作是在一张权值表中进行 lookup ，论文中作者强调他们这一步会将 Input Feture Vector 中的值与 Embedding 向量相乘。

Bi-Interaction Layer 层是这篇论文的创新，对 embedding 之后的特征两两之间做 element-wise product，并将结果相加得到一个 k 维（Embeding 大小）向量。这一步相当于对特征的二阶交叉，与 FM 类似，这个公式也能进行化简：

• $f_{B I}\left(\mathcal{V}{x}\right)=\sum{i=1}^{n} \sum_{j=i+1}^{n} x_{i} \mathbf{v}{i} \odot x{j} \mathbf{v}{j} =\frac{1}{2}\left[\left(\sum{i=1}^{n} x_{i} \mathbf{v}{i}\right)^{2}-\sum{i=1}^{n}\left(x_{i} \mathbf{v}_{i}\right)^{2}\right]$
  Hidden Layers 层利用常规的 DNN 学习高阶特征交叉

Prdiction Layer 层输出最终的结果：

• $$
  \begin{aligned} \hat{y}{N F M}(\mathbf{x}) &=w{0}+\sum_{i=1}^{n} w_{i} x_{i} +\mathbf{h}^{T} \sigma_{L}\left(\mathbf{W}{L}\left(\ldots \sigma{1}\left(\mathbf{W}{1} f{B I}\left(\mathcal{V}{x}\right)+\mathbf{b}{1}\right) \ldots\right)+\mathbf{b}_{L}\right) \end{aligned}
  $$

实验结果：

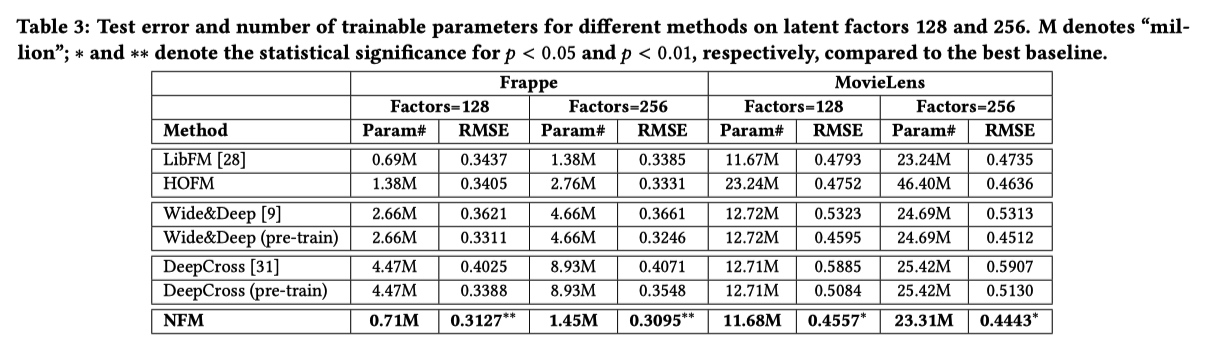
tags:: #HOFM