[[Abstract]]
- CTR prediction in real-world business is a difficult machine learning problem with large scale nonlinear sparse data. In this paper, we introduce an industrial strength solution with model named Large Scale Piece-wise Linear Model (LS-PLM). We formulate the learning problem with L1 and L2,1 regularizers, leading to a non-convex and non-smooth optimization problem. Then, we propose a novel algorithm to solve it efficiently, based on directional derivatives and quasi-Newton method. In addition, we design a distributed system which can run on hundreds of machines parallel and provides us with the industrial scalability. LS-PLM model can capture nonlinear patterns from massive sparse data, saving us from heavy feature engineering jobs. Since 2012, LS-PLM has become the main CTR prediction model in Alibaba’s online display advertising system, serving hundreds of millions users every day.
[[Attachments]]
分片线性方式对数据进行拟合,将空间分成多个区域,每个区域使用线性的方式进行拟合,最后的输出变为多个子区域预测值的加权平均。
相当于对多个区域做一个 [[Attention]]
结构与三层神经网络类似
Model
处理大规模稀疏非线性特征
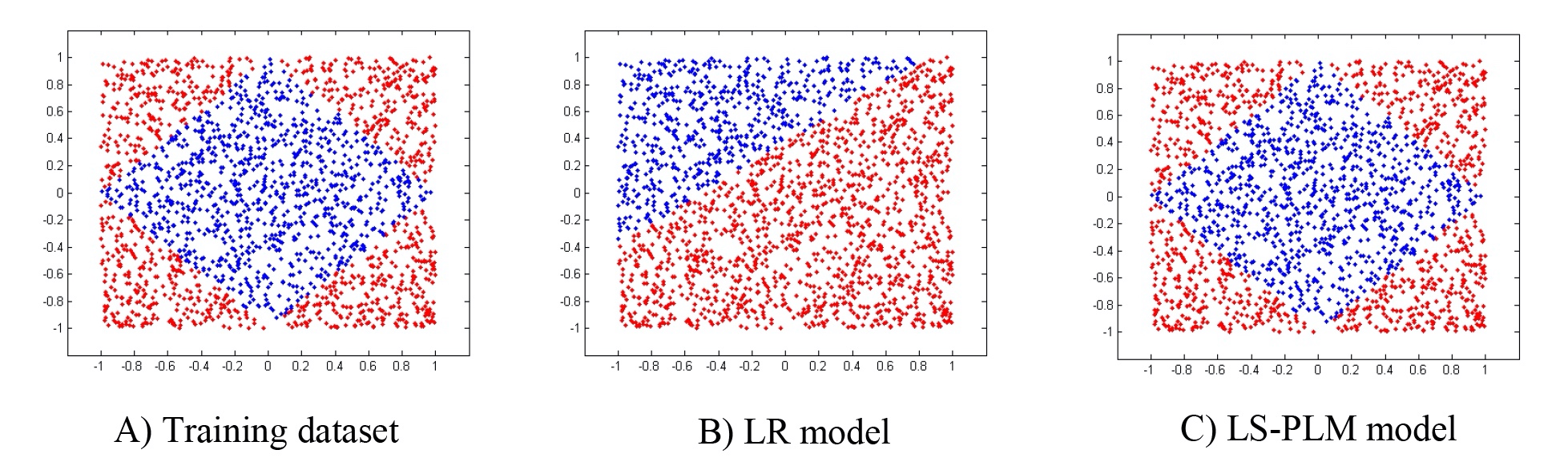
LS-PLM 模型学习数据的非线性特征。
question 为什么 LR 模型不能区分下面的数据,如何区分数据?[[SVM]][[FM]]
$$p(y=1 | x)=g\left(\sum_{j=1}^{m} \sigma\left(u_{j}^{T} x\right) \eta\left(w_{j}^{T} x\right)\right)$$
u 和 w 都是 d 维向量
m 为划分 region 数量
一般化使用:
$$p(y=1 | x)=\sum_{i=1}^{m} \frac{\exp \left(u_{i}^{T} x\right)}{\sum_{j=1}^{m} \exp \left(u_{j}^{T} x\right)} \cdot \frac{1}{1+\exp \left(-w_{i}^{T} x\right)}$$
可以把上面的模型看成是三层神经网络
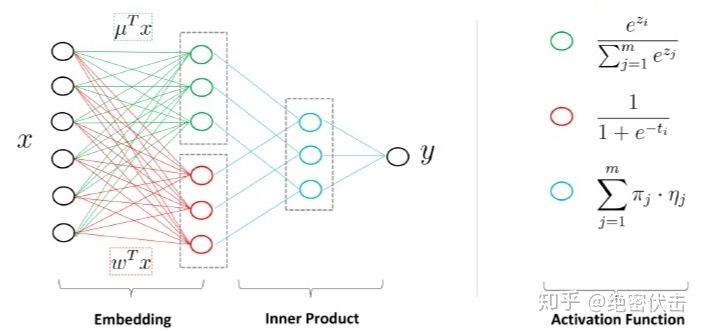
Regularization
$$\arg \min {\Theta} f(\Theta)=\operatorname{loss}(\Theta)+\lambda|\Theta|{2,1}+\beta|\Theta|_{1}$$
L1 和常规一样,保持参数的稀疏性。
L2 如下面的公式,对每一个 feature 的参数进行二阶正则,然后累加。最优化的过程中,L2 项越来越小,相当于做特征选择。每一个特征不止一个参数,只有某一个特征的全部参数都为 0 ,代表这个特征是没有用的。
$$|\Theta|{2,1}=\sum{i=1}^{d} \sqrt{\sum_{j=1}^{2 m} \theta_{i j}^{2}}$$
正则后的效果:
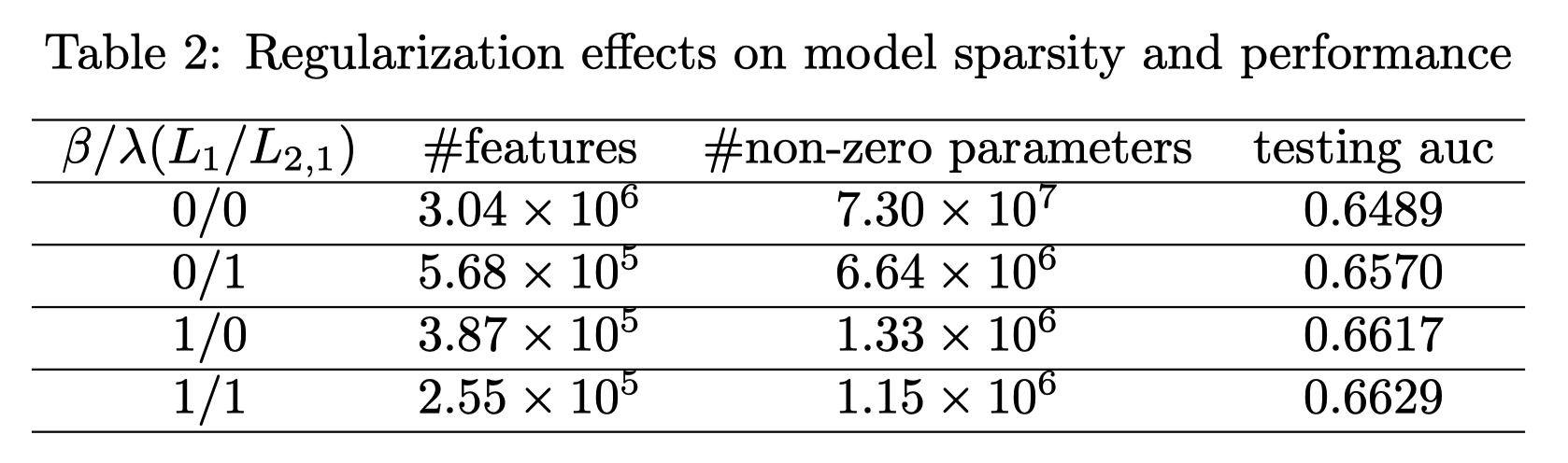
@wait 后面如何求解这损失函数以及工程实现待看。
[[Ref]]