Stable Unit Treatment Value Assumption [[稳定单元干预值假设]]#card

• 不同个体的潜在结果之间不会有交互影响

• 干预水平对所有个体一致

• 单元之间相互独立，一个单元受到的干预不会影响另外一个单元的潜在结果。举一个不满足的反例，某苹果手机降价后销量大涨，相关的手机壳等配件销量也随之上涨，苹果手机和手机壳等就不是独立的，类似地可以用GNN建模该关联。

• 干预形式是唯一的，对于同一种干预不存在能产生不同潜在结果的其他版本。举一个不满足的反例，如果将降价视为干预，打5折和打9折对销量的影响显然差异巨大，而应该将不同的折扣建模为多值干预。

[[No unmeasured confounders]] 没有未测量的混杂因子#card

• 可忽略性/非混淆假设（Ignorability / Unconfoundedness Assumption

• $W \perp \!\!\! \perp Y(W=0), Y(W=1) \mid X$

• 给定X，则分配机制与Y无关

• 如果两个个体的x一样，则无论W是什么，其潜在结果一样

• 如果两个个体的×一样，则无论潜在结果是什么，它们的分配机制都一样

• 背景变量包含了所有的混杂因子。如果背景变量仅包含了部分混杂因子，那就无法去除干净伪相关的影响，预测的因果效应就存在高低估问题。不过想要做到这点挺难的，有时候我们都不知道有哪些混杂因子，更别提把它们都包括进来。
  相同背景变量的单元无论受到何种干预其潜在结果也相同，并且无论潜在结果如何其受到的干预机制相同。

Positivity [[正值假设]]#card

• 干预是确定的，对于任何背景变量的单元，每一种干预的概率大于0。

• $P(W=w \mid X=X)>0 \quad \forall w$ and $x$

• common support / overlap

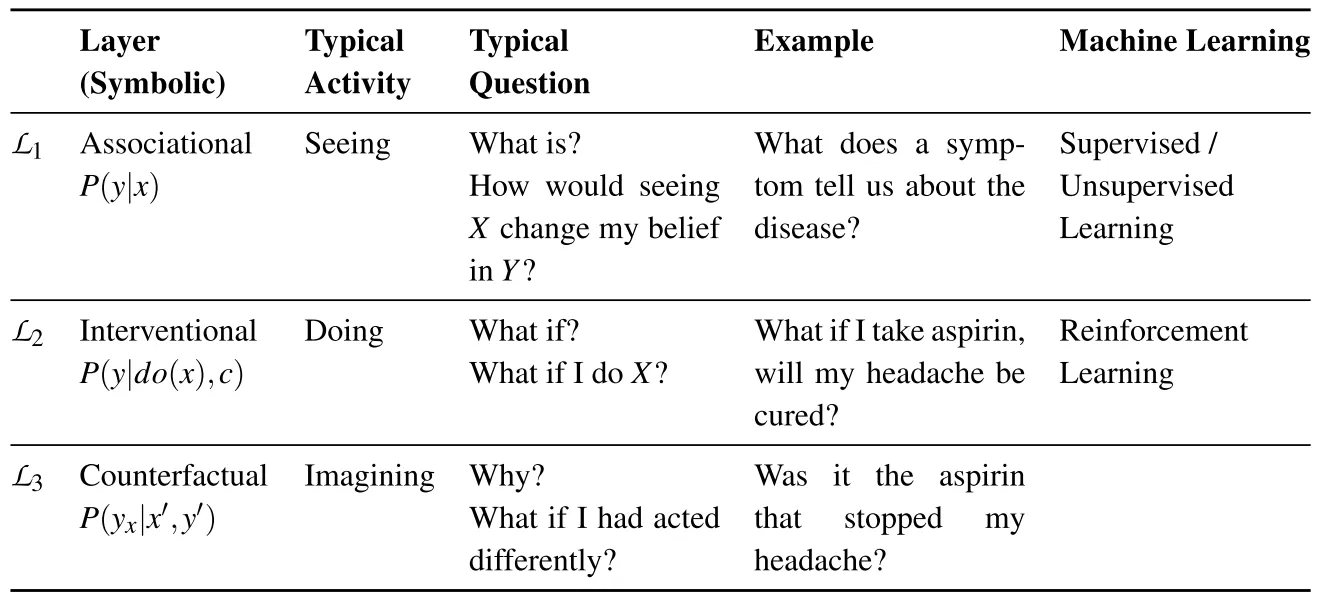
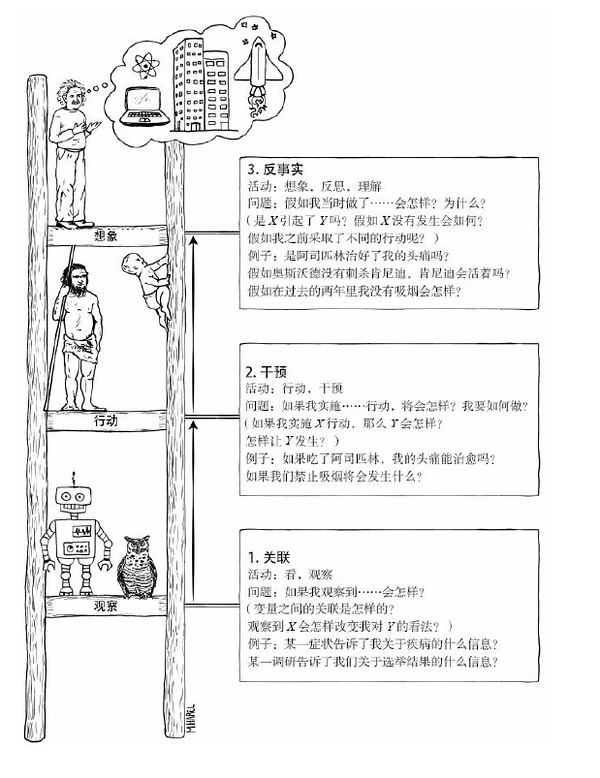
[[UPlift Model]] 目标是学习个体潜在弹性 $\tau=Y(1)-Y(0)$
，没有标签。

计算过程

• 数据集 $D=\left(Y_i^{\text {obs }}, W_i\right.$, score $\left._i\right)$

  • W 是样本所在的组，1 为实验组，0 为空白组

  • Y_obs 是观测到的样本响应信号

  • socre 是样本的 uplift 值

• 按 socre 从大到小排序，第 k 个的 uplift 值

  • $u(k)=\frac{R^T(D, k)}{N^T(D, k)}-\frac{R^C(D, k)}{N^C(D, k)}$

    • $R^T(D, k)=\sum Y_i^{o b s} \mathbb{I}\left(W_i=1\right)$ 排在前 k 个样本中属于实验组的人的响应之和

    • $R^C(D, k)=\sum Y_i^{o b s} \mathbb{I}\left(W_i=0\right)$ 空白组的人的响应之和

    • $N^T(D, k)=\sum \mathbb{I}\left(W_i=1\right)$ 前 k 实验组人数

    • $N^C(D, k)=\sum \mathbb{I}\left(W_i=0\right)$ 前 k 空白组人数

    • 避免实验组和对照组用户数量差别较大导致指标不可靠

    • 全量人群的 [[Average Treatment Effect]]

  • 含义：前 k 个样本中实验组平均产生的价值 - 前 k 个样本中空白组平均产生的价值

• 计算 $A U U C=\frac{S}{n * u(n)}$

  • $S=\sum_{k=1}^n(u(k) * k)$

    • $(u(k) * k)$ 代表前 k 个人产生的 uplift 值

Ref

• 实现 [[causalml]]

  • lift.plot x=k, y=u(k)

  • gain.plot x=k, y= k*u(k)

• 弹性模型的评测指标AUUC - 知乎

  • 画 [[auuc/code]]

  • auuc_score['random'] 值含义是什么？

    • 无规律排序下，实验组相对于控制组的期望增值

    • TODO 在大多数情况下，使用归一化的auuc_score(normalize=True)函数计算得到的random值应该接近0.5，gain.plot()画出的random应该是一条直线。原因是在多次随机排序下，期望增值应该是稳步上升的。

    • 假如random值不是0.5，图像不是直线时，这意味着什么？

      • 导致不是0.5的背后原因可能有很多，可以先分析下是不是以下三种情况。

        • 1.实验组和空白组不是平衡的，两者人群不是同质的，这时算AUUC没有很大的意义了，应该调平人群后再计算。

        • 2.样本的y值即响应信号的离群点比较多。

        • 3.样本量太小，无法支撑实验组和对照组的匹配。

      • 除此之外，还有一种情况是random值为-0.5，这时整体的ATE为负数，所有样本均为负弹，这时候uplift值不再是“收益”，更像是“花销”。

• [[@DiDi Food中的智能补贴实战漫谈]]

T/S/X-Learner [[@Meta-learners for Estimating Heterogeneous Treatment Effects using Machine Learning]]

• 适用情形：#card

  • 随机干预实验的数据，对于非随机的观测数据，可以结合下文的表示学习，实际上很多表示学习的模型框架就是以 T-Learner 为基础。T/S/X-Learner 本质上也是利用相似单元的事实结果进行反事实估计，只不过是把相似单元的事实结果编码进模型参数里了。

• [[S-Learner]]

• [[T-Learner]]

• [[S-Learner vs T-Learner]]

• [[X-Learner]]

[[R-Learner]]

[[Potential Outcome Framework 专有名词]]

[[Treatment Effect]]

• [[ITE]] 个体干预效果

• [[ATE]] Average Treatment Effect，针对全体用户

  • [[CATE]] 条件，给定条件下的全体用户

• [[ATT]] 实验组

[[Potential Outcome Framework 简化问题的三个假设]]

经典方法

• [[Re-weighting methods]] 解决的问题是控制组和治疗组的分布不同

• [[Matching methods]] 关键在于如何度量样本之间的相似性

• Tree-based Method - [[Causal Forest]] 在分裂最大化 ITE 方差

• [[Representation Learning Method]] 本质是对反事实进行预测

• [[Meta-Learner]]

倾向性评分是一个概率值（介于0和1之间），表示#card

• 在给定一组观测到的协变量（covariates，如年龄、性别、病史等）的情况下，某个个体被分配到处理组（而非对照组）的条件概率。

• 当前输入特征下用户被分配到实验组的概率

  • $e(x)=\operatorname{Pr}[T=1 \mid X=x]$

对于倾向性得分相同的一群用户，treatment 和特征是独立的，treatment 和潜在结果也是独立。

PCH Pearl’s Causal Hierarchy

因果关系者掌握三种不同层级的认知能力：观察能力（seeing）、行动能力（doing）和想象能力（imagining）。

第一层对应观察到的世界，第二层对应的是一个可被观察的美好新世界，第三层对应无法被观察到的世界。

• 第一层级是观察能力，具体而言是指发现环境中的规律的能力。在认知革命发生之前，这种能力为许多动物和早期人类所共有。

  • 关联：统计学，当前深度学习，依赖数据，缺乏灵活性和适应性

• 第二层级是行动能力，涉及预测对环境进行刻意改变后的结果，并根据预测结果选择行为方案以催生出自己期待的结果。

  • 干预比关联更高级，因为它不仅涉及被动观察，还涉及主动改变现状。

  • 干预：参考过去的数据，不能解决当前的行为。比如之前的涨价是由于其他原因导致的。AB实验

• 第三层想象能力

  • 反事实，对事件干预后进行反思

滴滴国际化外卖团队的文章，前几个月做补贴关业务的时候看过。文章链接：https://mp.weixin.qq.com/s/WU1iILMFdH3RZAbJKFU4WA

滴滴国际化外卖团队的文章，前几个月做补贴关业务的时候看过。文章链接：https://mp.weixin.qq.com/s/WU1iILMFdH3RZAbJKFU4WA