时间序列分析的核心是挖掘该序列中的自相关性

特征

• 趋势

• 季节变化

• 相关性 serial correlation

  • 自相关性是时间序列可以预测未来的前提

  • 波动聚类 volatility clustering

• 随机噪声

[[时间序列分解]]

• 从时间序列的波动中挖掘信息

• 核心

  • 数据序列本身是隐藏着规律的，不可预测的部分很小

  • 分解方法要合适，周期判断准确

• [[Python/package]] statsmodels.tsa.seasonal 中 seasonal_decompose

  • trend 趋势序列

  • seasonal 季节序列

  • resid 残差序列

[[平稳性]]

• [[ADF 检验]]

• [[ACF]]

  • graphics.tsa.plot_acf

• [[PACF]]

  • graphics.tsa.plot_pacf

• 相关图可以帮助判断模型是否合适

  • 自相关性

    • 原始时间序列与模型拟合的时间序列之间的残差应该近似于随机噪声

    • 标准的随机噪声的自相关满足 $\rho_0 = 1, \rho_k =1$

      • 任意不为 0 的间隔，随机噪声的自相关均为 0

[[传统时间序列预测]]

[[Linear Regression]] 预测

• 残差散点图

• [[R2 score]]评分指标

  • $R^2=1-\frac{S S_{r e s}}{S S_{t o t}}, S S_{r e s}=\sum\left(y_i-f_i\right)^2, S S_{t o t}=\sum\left(y_i-\bar{y}\right)^2$

  • fi预测，yi样本

  • SSres 残差平方和

  • SStot 真实值与其平均值的残差的平方和

  • 将拟合模型与数据均值相比较

    • R2=0 模型拟合和均值一样

    • R2 越接近于 1 说明模型效果越好

    • R2 < 0 说明拟合模型还不如均值模型

线性与非线性模型应用于同一时间序列

• [[ARIMA]] 从线性自相关角度进行建模

• 单时间序列 LSTM 从非线性自相关角度进行建模

• 多元 LR 从线性互相关角度进行建模

• 多元 LSTM 从非线性互相关角度进行建模

[[TCN]]

Ref

• 时间序列分析 自协方差/自相关系数/偏自相关系数 - 知乎 (zhihu.com)

• 时间序列分析（1） 基本概念与实战 - 知乎 (zhihu.com)

• 时间序列分析（2） ARIMA 模型 - 知乎 (zhihu.com)

香港中文大学曾爱玲文章，在长时间序列预测问题上使用线性模型打败基于 Transformer 的模型，并对已有模型的能力进行实验分析（灵魂7问，强烈推荐好好读一下！）。

[[Abstract]]

• Transformers have achieved superior performances in many tasks in natural language processing and computer vision, which also triggered great interests in the time series community.

• Among multiple advantages of transformers, the ability to capture long-range dependencies and interactions is especially attractive for time series modeling, leading to exciting progress in various time series applications.

  • In this paper, we systematically review transformer schemes for time series modeling by highlighting their strengths as well as limitations. In particular, we examine the development of time series transformers in two perspectives.

    • From the perspective of network structure, we summarize the adaptations and modification that have been made to transformer in order to accommodate the challenges in time series analysis.

    • From the perspective of applications, we categorize time series transformers based on common tasks including forecasting, anomaly detection, and classification.

  • Empirically, we perform robust analysis, model size analysis, and seasonal-trend decomposition analysis to study how transformers perform in time series.

  • Finally, we discuss and suggest future directions to provide useful research guidance.

• A corresponding resource list which will be continuously updated can be found in the GitHub repository1.

[[Attachments]]

• Transformers in Time Series-2022.pdf

Input Encoding and Positional Encoding

• Absolute Positional Encoding

• Relative Positional Encoding

• Hybrid positional encodings

Network Modifications for Time Series

• [[Positional Encoding]]

  • Vanilla Positional Encoding

  • Learnable Positional Encoding

    • [[A transformer-based framework for multivariate time series representation learning]] introduce an embedding layer in Transformer that learn embedding vectors for each position index jointly with other model parameters.

    • [[Temporal Fusion Transformers]] 使用 LSTM 对位置进行编码，更好适应时序预测任务

  • Timestamp Encoding

    • calendar timestamps(hours, minute…) 和 special timestamps (holidays and events)

    • [[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting]] [[Autoformer]] [[FEDformer]] 将 timestamps 特征转换成 embedding 通过网络学习

    • 如何生成好的 timestamp encoding 比较依赖人工先验

• Attention Module

  • 提升 self-attention 计算效率

  + [[LogTrans]] [ Li et al., 2019 ] and [\[\[Pyraformer\]\]](/post/logseq/%40Pyraformer%3A%20Low-Complexity%20Pyramidal%20Attention%20for%20Long-Range%20Time%20Series%20Modeling%20and%20Forecasting.html) explicitly introducing a sparsity bias

  + 移除 self-attention 矩阵部分值 [\[\[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting\]\]](/post/logseq/%40Informer%3A%20Beyond%20Efficient%20Transformer%20for%20Long%20Sequence%20Time-Series%20Forecasting.html) [[FEDformer]]

• Architecture Level

  • renovate transformer

  • hierarchical architecture 分层结构

    • 针对考虑到时间序列的多分辨率(多周期，多趋势叠加)

      • [[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting]] max-pooling layer

      • [[Pyraformer]] C-ary tree base attention mechanism

        • nodes at the finest scale correspond to the original time series

        • nodes in the coarser scales represent series at lower resolutions

        • both intra-scale and inter-scale attentions in order to better capture temporal dependencies across different resolutions

Applications of Time Series Transformers

• Forecasting

  • Time Series Forecasting

    • [[LogTrans]]

      • proposed convolutional self-attention by employing causal convolutions to generate queries and keys in the self-attention layer 因果卷积引入子注意力计算

      • a Logsparse mask

    • [[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting]]

    • AST [[Adversarial sparse transformer for time series forecasting]]

      • 使用生成对抗编码器-解码器架训练用于时间序列预测的稀疏 Transformer 模型

      • 对抗训练可以直接塑造网络的输出来改善预测效果，避免逐步预测带来的累积误差

        • directly shaping the output distribution of network to avoid the error accumulation through one-step ahead inference

    • [[Autoformer]]

      • simple seasonaltrend decomposition architecture 简单季节性趋势分解架构

      • an auto-correlation mechanism working as an attention module 自相关机制注意力模块 $O(L\log L)$

        • measures the time-delay similarity between inputs signal and aggregate the top-k similar sub-series to produce the output

    • [[FEDformer]]

      • 利用 [[Fourier transform]] 和 [[Wavelet transform]] 处理 frequency domain 频域中的注意力操作

        • linear complexity

    • [[@Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting]]

      • multi-horizon forecasting model with static covariate encoders, gating feature selection and temporal self-attention decoder

    • [[SSDNet]] [[ProTran]]

      • combine Transformer with state space models to provide probabilistic forecasts 提供概率预测

    • [[Pyraformer]]

      • hierarchical pyramidal attention module with binary tree following path

      • 分层金字塔注意力模块，二叉树

    • [[Aliformer]]

      • Knowledge-guided attention

  • Spatio-Temporal Forecasting [[Traffic Flow Forecasting]]

    • Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting

      • self attention module to capture temporal-temporal dependencies 时序特征

      • Graph neural network module to capture spatial dependencies 空间特征

    • Spatialtemporal Transformer

      • 空间 transformer 辅助图卷积网络来捕获空间依赖关系

    • Spatio-temporal graph Transformer

      • 基于注意力的图卷积机制

  • Event Forecasting

    • temporal point processes (TPP)

• Anomaly Detection

• Classification

  • [[GTN]]

Experimental Evaluation and Discussion

模型鲁棒性、模型大小以及对时序季节性和趋势捕捉能力

• robustness analysis, model size analysis, and

seasonal-trend decomposition analysis

• seasonal-trend decomposition 是 transformer 解决时序预测的重要组成部分

• 所有模型加上 moving average trend decomposition architecture proposed 结构后，和原始模型相比效果都获得提升

Future Research Opportunities

• [[inductive bias]] for Time Series Transformers

  • 避免过拟合，训练 transformer 需要大量数据。

  • 时序数据具有 seasonal/periodic and trend patterns

  • 将对于时序数据模型的理解和特定任务的特征做为归纳偏置引入 transformer

• [[GNN]]

  • 增强对于空间依赖和多维度之间的关系建模能力

• [[预训练]]

  • 目前针对时间序列的预训练 transformer 集中在时序分类任务中

• [[Neural architecture search]]

  • 如果构建高效的 transformer 结构

Ref

• TODO [[A transformer-based framework for multivariate time series representation learning]]

• TODO [[Adversarial sparse transformer for time series forecasting]]

• DONE [[@Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting]]
  completed:: [[2022/11/08]]

• TODO [[SSDNet]]

• TODO [[ProTran]]

• [[LogSparse Transformer]]

• Transformer应用于时序任务的综述【2022by阿里达摩院】 - 知乎 (zhihu.com)

  • 影响预测效果的细节

    • 训练

    • Encoder 间的特征工程

[[Attachments]]

• Autoformer_2022_Wu.pdf

关键信息

• [[Long Term Series Forecasting]] [[时间序列分解]]

核心贡献

• Autoformer as a novel decomposition architecture with an Auto-Correlation mechanism
  ls-type:: annotation
  hl-page:: 1
  hl-color:: yellow
  [[Auto-Correlation Mechanism]] 自相关机制，代替点向连接的注意力机制，实现序列级连接和较低复杂度

  • 序列级别依赖发现以及表示聚合 conducts the dependencies discovery and representation aggregation at the sub-series level.
    ls-type:: annotation
    hl-page:: 1
    hl-color:: yellow

• Decomposition Architecture 深度分解架构，从复杂时间模式种分解出可预测性更强的成分

  • 推理复杂时间模式 intricate temporal patterns
    ls-type:: annotation
    hl-page:: 2
    hl-color:: yellow

    • process the complex time series and extract more predictable components.
      ls-type:: annotation
      hl-page:: 2
      hl-color:: yellow

    • 常规对前向数据进行分解，忽视未来可能发生的分解组件之间的潜在交互作用

      • This common usage limits the capabilities of decomposition and overlooks the potential future interactions among decomposed components.
        ls-type:: annotation
        hl-page:: 2
        hl-color:: blue

    • 分解可以解开纠缠的时间模式并突出时间序列的固有属性 can ravel out the entangled temporal patterns and highlight the inherent properties of time series
      ls-type:: annotation
      hl-page:: 2
      hl-color:: blue

    • 对子序列进行分解，基于时间序列周期性导出的过程相似性构建一种系列级连接 sub-series at the same phase position among periods often present similar temporal processes
      ls-type:: annotation
      hl-page:: 2
      hl-color:: yellow

    • 逐步分解整个预测过程中的隐藏序列，包括过去的序列和预测的中间结果

      • decompose the hidden series throughout the whole forecasting process, including both the past series and the predicted intermediate results.
        ls-type:: annotation
        hl-page:: 3
        hl-color:: yellow

核心问题

• 原始序列中各种趋势信息比较混乱，无法在长时间序列中发现时间依赖

  • unreliable to discover the temporal dependencies directly from the long-term time series because the dependencies can be obscured by entangled temporal patterns.
    ls-type:: annotation
    hl-page:: 1
    hl-color:: green

  • 需要处理复杂的时间模式，打破计算效率和信息利用的瓶颈 handling intricate temporal patterns and breaking the bottleneck of computation efficiency and information utilization.
    ls-type:: annotation
    hl-page:: 3
    hl-color:: blue

  • 待预测序列长度远远大于输入长度

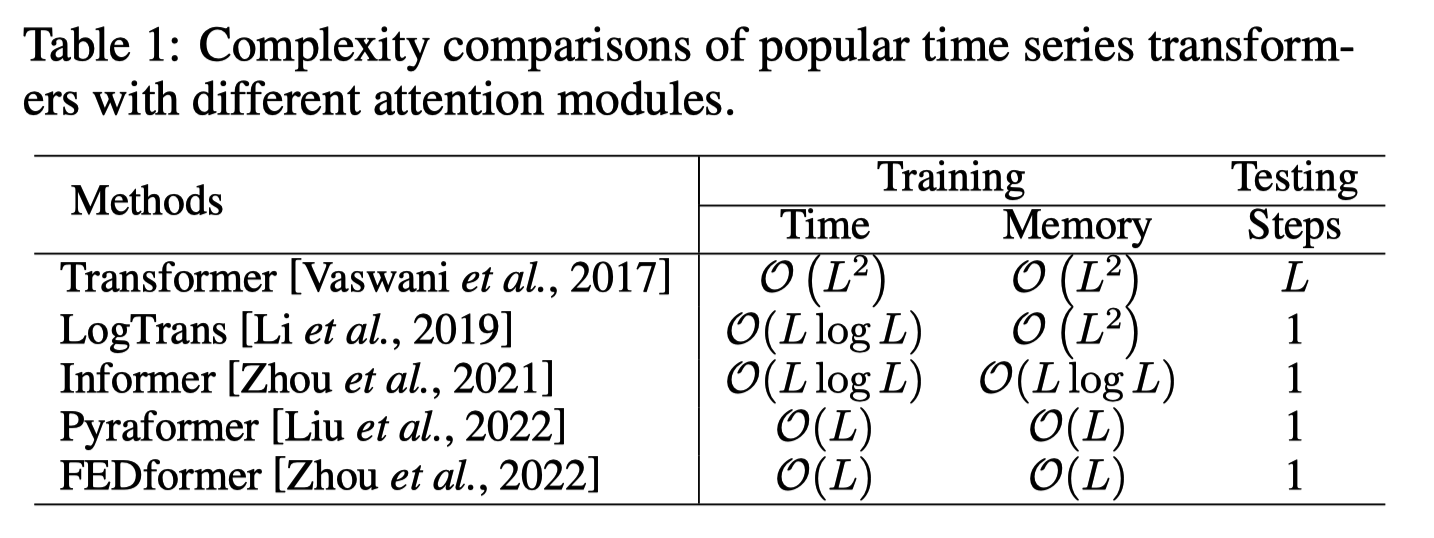
• Transformer 平方级别复杂度

  • 之前方法尝试使用稀疏 self-attention mproving self-attention to a sparse version
    ls-type:: annotation
    hl-page:: 1
    hl-color:: green

    • 稀疏注意力机制将造成信息的丢失，成为长时间序列预测的瓶颈

  • these models still utilize the point-wise representation aggregation
    ls-type:: annotation
    hl-page:: 1
    hl-color:: blue

• Transformer point-wise 维度聚合

  • self-attention 来捕捉时刻间的依赖

    • 难以直接发现可靠的时间依赖

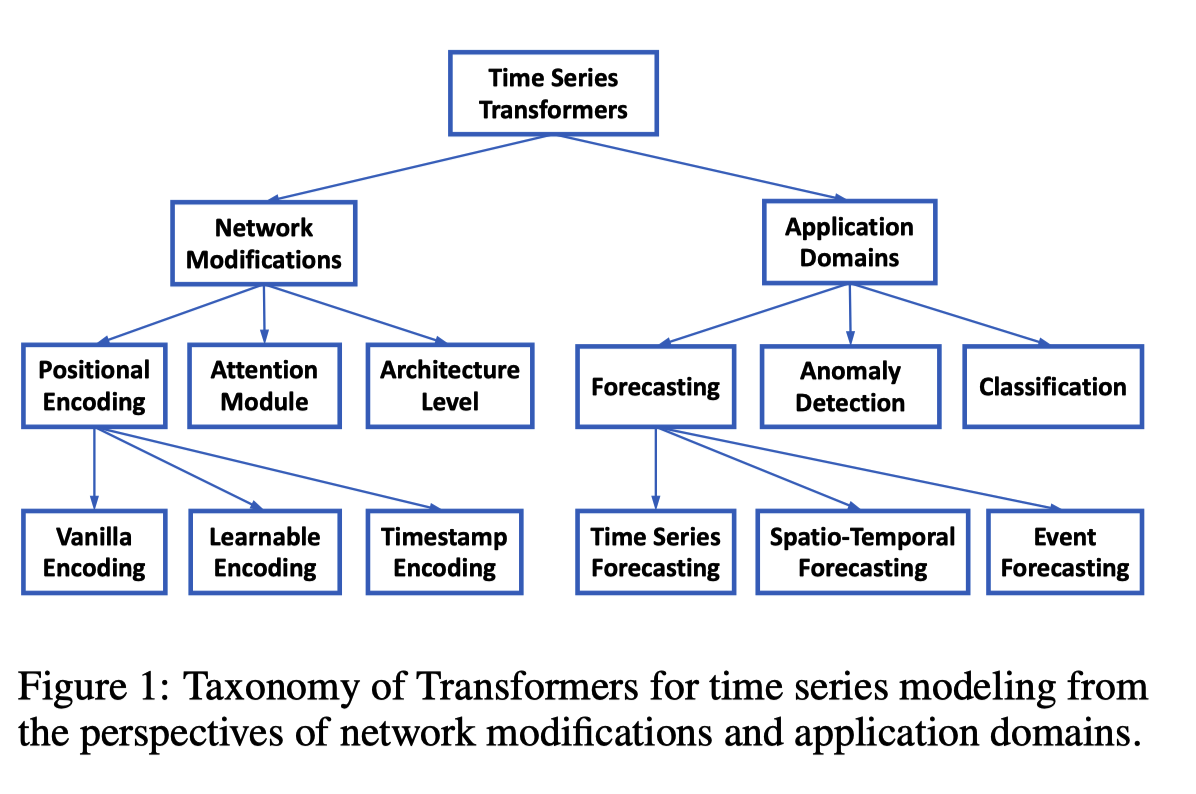
相关工作

• 之前方法集中在 recurrent connections, temporal attention or causal convolution.
  ls-type:: annotation
  hl-page:: 2
  hl-color:: blue

  • [[DeepAR]] 自回归 + RNN 建模未来序列的概率分布

    • combines autoregressive methods and RNNs to model the probabilistic distribution of future series.
      ls-type:: annotation
      hl-page:: 2
      hl-color:: blue

  • [[LSTNet]] CNNs + ResNet 捕捉 short-term 和 long-term temporal patterns

  • [[TCN]]

• Transformer 类方法

  • [[Reformer]] [[local-sensitive hashing attention]] #mark/paper

  • [[Informer]] KL + [[ProbSparse Attention]]

• Decomposition of Time Series

  • 将原始时间序列分解成多个序列，新序列更容易预测

    • each representing one of the underlying categories of patterns that are more predictable.
      ls-type:: annotation
      hl-page:: 3
      hl-color:: blue

  • [[Prophet]] with trend-seasonality decomposition

  • [[N-BEATS]] with basis expansion

  • [[DeepGLO]] with matrix decomposition

  • 缺点

    • 简单分解限制

      • limited by the plain decomposition effect of historical series
        ls-type:: annotation
        hl-page:: 3
        hl-color:: yellow

    • 忽视层次交互

      • overlooks the hierarchical interaction between the underlying patterns of series in the long-term future.
        ls-type:: annotation
        hl-page:: 3
        hl-color:: yellow

      • 预测问题未来的不可知性，通常方法先对过去序列进行分解，再分别预测，这会造成预测结果受限于分解效果，并且忽视了未来各个组分之间的相互作用。

解决方法

• Decomposition Architecture
  ls-type:: annotation
  hl-page:: 3
  hl-color:: yellow

  • [:span]
    ls-type:: annotation
    hl-page:: 4
    hl-color:: yellow

tags:: #[[Model Architecture]] [[Encoder-Decoder]]

+ series decomposition block

ls-type:: annotation
hl-page:: 3
hl-color:: yellow
保留周期部分

  + 序列分解成趋势项和周期项部分 separate the series into trend-cyclical and seasonal parts.

ls-type:: annotation
hl-page:: 3
hl-color:: yellow

  + 在预测过程中，模型交替进行预测结果优化和序列分解，从隐藏变量中逐步分离趋势项与周期项

  + 逐步从预测的中间隐藏变量中提取长期稳定的趋势 xtract the long-term stationary trend from predicted intermediate hidden variables progressively. 

ls-type:: annotation
hl-page:: 3
hl-color:: yellow

  + 使用 [[Moving Average]] 平滑周期性、突出趋势项 smooth out periodic fluctuations and highlight the long-term trends

ls-type:: annotation
hl-page:: 3
hl-color:: yellow

    + $\mathcal{X}_{\mathrm{s}}, \mathcal{X}_{\mathrm{t}}=\operatorname{SeriesDecomp}(\mathcal{X})$

      + $\begin{aligned} & \mathcal{X}_{\mathrm{t}}=\operatorname{Avg} \operatorname{Pool}(\operatorname{Padding}(\mathcal{X})) \\ & \mathcal{X}_{\mathrm{s}}=\mathcal{X}-\mathcal{X}_{\mathrm{t}}\end{aligned}$

      + xs seasonal

      + xt trend-cyclial part

+ [[Encoder]]

  + Encoder 输入过去 I 步 $\mathcal{X}_{\mathrm{en}} \in \mathbb{R}^{I \times d}$

  + 建模周期性部分，逐步消除趋势项（在 decoder 中通过累积得到） focuses on the seasonal part modeling

ls-type:: annotation
hl-page:: 4
hl-color:: yellow

    + 当成 decoder 的交叉信息 be used as the cross information to help the decoder refine prediction results

ls-type:: annotation
hl-page:: 4
hl-color:: yellow

  + 流程

    + _ the eliminated trend part

ls-type:: annotation
hl-page:: 4
hl-color:: red
消除趋势项

    + $\begin{aligned} & \mathcal{S}_{\text {en }}^{l, 1},_{-}=\operatorname{SeriesDecomp}\left(\text { Auto-Correlation }\left(\mathcal{X}_{\text {en }}^{l-1}\right)+\mathcal{X}_{\text {en }}^{l-1}\right) \\ & \mathcal{S}_{\text {en }}^{l, 2},_{-}=\operatorname{SeriesDecomp}\left(\text { FeedForward }\left(\mathcal{S}_{\text {en }}^{l, 1}\right)+\mathcal{S}_{\text {en }}^{l, 1}\right)\end{aligned}$

+ [[Decoder]]  分解对趋势项与周期项建模

  + 一半过去信息 + 填充

    + $\begin{aligned} \mathcal{X}_{\text {ens }}, \mathcal{X}_{\text {ent }} & =\operatorname{SeriesDecomp}\left(\mathcal{X}_{\text {en } \frac{I}{2}: I}\right) \\ \mathcal{X}_{\text {des }} & =\operatorname{Concat}\left(\mathcal{X}_{\text {ens }}, \mathcal{X}_0\right) \\ \mathcal{X}_{\text {det }} & =\operatorname{Concat}\left(\mathcal{X}_{\text {ent }}, \mathcal{X}_{\text {Mean }}\right),\end{aligned}$

    + seasonal part $\mathcal{X}_{\mathrm{des}} \in \mathbb{R}^{\left(\frac{1}{2}+O\right) \times d}$

    + trend-cyclical part $\mathcal{X}_{\mathrm{det}} \in \mathbb{R}^{\left(\frac{1}{2}+O\right) \times d}$

  + 趋势-周期累积结构 the accumulation structure for trend-cyclical components

ls-type:: annotation
hl-page:: 4
hl-color:: yellow

    + 从中间隐变量提取潜在趋势，使得模型可以逐步改进趋势预测并且消除干扰信息，以便于在自相关性中发现基于周期的依赖关系。

    + 其中，对于周期项，自相关机制利用序列的周期性质，聚合不同周期中具有相似过程的子序列；

    + Note that the model extracts the potential trend from the intermediate hidden variables during the decoder, allowing Autoformer to progressively refine the trend prediction and eliminate interference information for period-based dependencies discovery in Auto-Correlation. 

ls-type:: annotation
hl-page:: 4
hl-color:: red

  + the stacked Auto-Correlation mechanism for seasonal component

ls-type:: annotation
hl-page:: 4
hl-color:: yellow

  + 流程

    + $\begin{aligned} \mathcal{S}_{\mathrm{de}}^{l, 1}, \mathcal{T}_{\mathrm{de}}^{l, 1} & =\operatorname{SeriesDecomp}\left(\text { Auto-Correlation }\left(\mathcal{X}_{\mathrm{de}}^{l-1}\right)+\mathcal{X}_{\mathrm{de}}^{l-1}\right) \\ \mathcal{S}_{\mathrm{de}}^{l, 2}, \mathcal{T}_{\mathrm{de}}^{l, 2} & =\operatorname{SeriesDecomp}\left(\text { Auto-Correlation }\left(\mathcal{S}_{\mathrm{de}}^{l, 1}, \mathcal{X}_{\mathrm{en}}^N\right)+\mathcal{S}_{\mathrm{de}}^{l, 1}\right) \\ \mathcal{S}_{\mathrm{de}}^{l, 3}, \mathcal{T}_{\mathrm{de}}^{l, 3} & =\operatorname{SeriesDecomp}\left(\text { FeedForward }\left(\mathcal{S}_{\mathrm{de}}^{l, 2}\right)+\mathcal{S}_{\mathrm{de}}^{l, 2}\right) \end{aligned}$

    + 趋势项，通过累积的方式逐步从预测的隐变量中提取出趋势信息

      + ${\mathcal{T}_{\mathrm{de}}^l =\mathcal{T}_{\mathrm{de}}^{l-1}+\mathcal{W}_{l, 1} * \mathcal{T}_{\mathrm{de}}^{l, 1}+\mathcal{W}_{l, 2} * \mathcal{T}_{\mathrm{de}}^{l, 2}+\mathcal{W}_{l, 3} * \mathcal{T}_{\mathrm{de}}^{l, 3}}$

• [[Auto-Correlation Mechanism]]

  • [:span]
    ls-type:: annotation
    hl-page:: 5
    hl-color:: yellow

  • 高效的序列级连接，从而扩展信息效用

  • Period-based dependencies 基于周期的依赖发现

    • 不同周期相同相位之间通常表现出相似的子过程 same phase position among periods naturally provides similar sub-processes.
      ls-type:: annotation
      hl-page:: 5
      hl-color:: yellow

    • [[Stochastic process theory]] discrete-time process 的 [[autocorrelation]]

      • $\mathcal{R}_{\mathcal{X} \mathcal{X}}(\tau)=\lim _{L \rightarrow \infty} \frac{1}{L} \sum_{t=1}^L \mathcal{X}_t \mathcal{X}_{t-\tau}$

      • $\mathcal{R}_{\mathcal{X} \mathcal{X}}(\tau)$ 代表序列 $\{ \mathcal{X}_t \}$ 和 $\tau$ 延迟 $\{ \mathcal{X}_{t - \tau} \}$ 之间的相似性

      • 将这种时延相似性看作未归一化的周期预估的置信度，即周期长度为 \tau 的置信度为 $\mathcal{R}(\tau)$

        • 假设周期为 \tau， $\mathcal{X}_{\tau: L-1}$ 与 $\mathcal{X}_{0: L-\tau-1}$ 会极为相似

    • 取最相关 k 个长度 choose the most possible k period lengths
      ls-type:: annotation
      hl-page:: 5
      hl-color:: yellow

  • Time delay aggregation 时延信息聚合

    • 该部分聚合组序列 oll the series based on selected time delay
      ls-type:: annotation
      hl-page:: 5
      hl-color:: yellow

    • 相似的子序列信息进行聚合

    • 流程

      • 计算 top k=clogL 个长度

        • $\tau_1, \cdots, \tau_k=\underset{\tau \in\{1, \cdots, L\}}{\arg \operatorname{Topk}}\left(\mathcal{R}_{\mathcal{Q}, \mathcal{K}}(\tau)\right) \\$

      • 计算长度后计算相关性，然后求 softmax

        • $\widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_1\right), \cdots, \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_k\right)=\operatorname{SoftMax}\left(\mathcal{R}_{\mathcal{Q}, \mathcal{K}}\left(\tau_1\right), \cdots, \mathcal{R}_{\mathcal{Q}, \mathcal{K}}\left(\tau_k\right)\right) \\$

      • Roll 进行信息对齐，$\mathcal{X}_{0: L-\tau-1}$ 移到序列最前面，$\mathcal{X}_{0: L-\tau-1}$ 和 $\mathcal{X}_{\tau: L-1}$ 保存着相似的趋势信息

        • during which elements that are shifted beyond the first position are re-introduced at the last position
          ls-type:: annotation
          hl-page:: 5
          hl-color:: red

        • $\begin{aligned}\text { Auto-Correlation }(\mathcal{Q}, \mathcal{K}, \mathcal{V})=\sum_{i=1}^k \operatorname{Roll}\left(\mathcal{V}, \tau_i\right) \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_i\right) \end{aligned}$

    • 多头

      • $\begin{aligned} \text { MultiHead }(\mathcal{Q}, \mathcal{K}, \mathcal{V}) & =\mathcal{W}_{\text {output }} * \text { Concat }\left(\operatorname{head}_1, \cdots, \text { head }_h\right) \\ \text { where } \text { head }_i & =\text { Auto-Correlation }\left(\mathcal{Q}_i, \mathcal{K}_i, \mathcal{V}_i\right)\end{aligned}$

    • 复杂度 $\mathcal{O}(L \log L)$

      • 计算 $\tau \in [1, L)$ 的相关性

      • Wiener-Khinchin 理论，自相关信息可以使用[[快速傅里叶变换]] Fast Fourier Transforms
        ls-type:: annotation
        hl-page:: 6
        hl-color:: yellow
        得到

  • 与其他方法对比

    • [:span]
      ls-type:: annotation
      hl-page:: 6
      hl-color:: yellow

  • 序列级高效连接

  • self-attention family only calculates the relation between scattered points
    ls-type:: annotation
    hl-page:: 6
    hl-color:: blue

  • 我们采用时间延迟块来聚合底层周期中相似的子序列。 we adopt the time delay block to aggregate the similar sub-series from underlying periods.
    ls-type:: annotation
    hl-page:: 6
    hl-color:: yellow

实验结论

• 参数设置

  • ADAM + early stopped

  • Autoformer contains 2 encoder layers and 1 decoder layer.
    ls-type:: annotation
    hl-page:: 7
    hl-color:: yellow

• 对比

  • Informer [ 48 ], Reformer [23 ], LogTrans [26 ], two RNN-based models: LSTNet [ 25], LSTM [ 17] and CNN-based TCN [ 4] as baselines.
    ls-type:: annotation
    hl-page:: 7
    hl-color:: yellow

  • N-BEATS[ 29 ], DeepAR [34 ], Prophet [ 39 ] and ARMIA
    ls-type:: annotation
    hl-page:: 7
    hl-color:: yellow

• 实验结果

  • 预测方式 前 96 预测后 96

    • we fix the input length and evaluate models with a wide range of prediction lengths: 96, 192, 336, 720.
      ls-type:: annotation
      hl-page:: 8
      hl-color:: yellow

  • [[multivariate]]

    • 训练变长预测表现变化也平稳 we can also find that the performance of Autoformer changes quite steadily as the prediction length O increases
      ls-type:: annotation
      hl-page:: 8
      hl-color:: yellow

    • [:span]
      ls-type:: annotation
      hl-page:: 7
      hl-color:: yellow

  • Univariate results
    ls-type:: annotation
    hl-page:: 8
    hl-color:: yellow
    单变量

    • . This situation of ARIMA can be benefited from its inherent capacity for non-stationary economic data but is limited by the intricate temporal patterns of real-world series.
      ls-type:: annotation
      hl-page:: 8
      hl-color:: yellow

    • [:span]
      ls-type:: annotation
      hl-page:: 8
      hl-color:: yellow

• [[Ablation Study]]

  • Decomposition architecture
    ls-type:: annotation
    hl-page:: 8
    hl-color:: yellow

    • 具有较好的通用性，其他模型加分解结构效果有提升，预测时效的延长，效果提升更明显

      • 减少复杂模式引起的干扰 our method can generalize to other models and release the capacity of other dependencies learning mechanisms, alleviate the distraction caused by intricate patterns
        ls-type:: annotation
        hl-page:: 9
        hl-color:: yellow

    • 对比深度分解架构和先分解再使用两个模型预测的方式，后者参数多，但是表现不好。

    • [:span]
      ls-type:: annotation
      hl-page:: 8
      hl-color:: yellow

  • Auto-Correlation vs. self-attention family
    ls-type:: annotation
    hl-page:: 9
    hl-color:: yellow

    • 效果超过 full attention，序列级别建模带来的收益

    • 可以预测更长序列

    • [:span]
      ls-type:: annotation
      hl-page:: 9
      hl-color:: yellow

• Model Analysis
  ls-type:: annotation
  hl-page:: 9
  hl-color:: yellow

  • time series decomposition

    • 随着序列分解单元的数量增加，模型学到的趋势项会越来月接近数据的正式结果，周期项可以更好的捕捉序列变化情况。

    • [:span]
      ls-type:: annotation
      hl-page:: 9
      hl-color:: yellow

  • Dependencies learning

    • 找到的注意力更合理 Autoformer can discover the relevant information more sufficiently and precisely.
      ls-type:: annotation
      hl-page:: 9
      hl-color:: yellow

    • 模型自相关机制可以正确发掘出每个周期的下降过程，没有误识别和漏识别，注意力机制存在错误和漏缺

    • [:span]
      ls-type:: annotation
      hl-page:: 10
      hl-color:: yellow

  • Complex seasonality modeling
    ls-type:: annotation
    hl-page:: 9
    hl-color:: yellow

    • 学习到的长度有意义 Autoformer can capture the complex seasonalities of real-world series from deep representations and further provide a human-interpretable prediction.
      ls-type:: annotation
      hl-page:: 10
      hl-color:: yellow

    • 高的部分说明有对应的周期性

    • [:span]
      ls-type:: annotation
      hl-page:: 10
      hl-color:: yellow

  • Efficiency analysis

读后总结

[[Autoformer Code]]

[[Abstract]]

• Many real-world applications require the prediction of long sequence time-series, such as electricity consumption planning. Long sequence time-series forecasting (LSTF) demands a high prediction capacity of the model, which is the ability to capture precise long-range dependency coupling between output and input efficiently. Recent studies have shown the potential of Transformer to increase the prediction capacity. However, there are several severe issues with Transformer that prevent it from being directly applicable to LSTF, including quadratic time complexity, high memory usage, and inherent limitation of the encoder-decoder architecture. To address these issues, we design an efficient transformer-based model for LSTF, named Informer, with three distinctive characteristics: (i) a ProbSparse self-attention mechanism, which achieves O(L log L) in time complexity and memory usage, and has comparable performance on sequences’ dependency alignment. (ii) the self-attention distilling highlights dominating attention by halving cascading layer input, and efficiently handles extreme long input sequences. (iii) the generative style decoder, while conceptually simple, predicts the long time-series sequences at one forward operation rather than a step-by-step way, which drastically improves the inference speed of long-sequence predictions. Extensive experiments on four large-scale datasets demonstrate that Informer significantly outperforms existing methods and provides a new solution to the LSTF problem.

[[Attachments]]

• Informer_2021_Zhou.pdf

Long sequence [[Time Series Forecasting]] (LSTF)

• 长序列时间序列预测需要模型能够有效捕捉输出和输入之间精确的 long-range dependency coupling

LSTF 中使用 [[Transformer]] 需要解决的问题 #card #incremental

• self-attention 计算复杂度 $O(L^2)$

• 多层 encoder/decoder 结构内存增长

• dynamic decoding 方式预测耗时长

网络结构

ProbSparse self-attention

• 替换 inner product self-attention

  • [[Sparse Transformer]] 结合行输入和列输出

  • [[LogSparse Transformer]] cyclical pattern

  • [[Reformer]] locally-sensitive hashing(LSH) self-attention

  • [[Linformer]]

  • [[Transformer-XL]] [[Compressive Transformer]] use auxiliary hidden states to capture long-range dependency

  • [[Longformer]]

• 其他优化 self-attention 工作存在的问题

  • 缺少理论分析

  • 对于 multi-head self-attention 每个 head 都采用相同的优化策略

• self-attention 点积结果服从 long tail distribution

  • 较少点积对贡献绝大部分的注意力得分

  • 现实含义：序列中某个元素一般只会和少数几个元素具有较高的相似性/关联性

• 第 i 个 query 用 $q_i$ 表示

  • $\mathcal{A}\left(q_i, K, V\right)=\sum_j \frac{f\left(q_i, k_j\right)}{\sum_l f\left(q_i, k_l\right)} v_j=\mathbb{E}_{p\left(k_j \mid q_i\right)}\left[v_j\right]$

  • $p\left(k_j \mid q_i\right)=\frac{k\left(q_i, k_j\right)}{\sum_l f\left(q_i, k_l\right)}$

  • $k\left(q_i, k_j\right)=\exp \left(\frac{q_i k_j^T}{\sqrt{d}}\right)$

• query 稀疏性判断方法

  • $p(k_j|q_j)$ 和[[均匀分布]] q 的 [[KL Divergence]]

    • q 是均分分布，相等于每个 key 的概率都是 $\frac{1}{L}$

    • 如果 query 得到的分布类似于均匀分布，每个概率值都趋近于 $\frac{1}{L}$，值很小，这样的 query 不会提供什么价值。

    • p 和 q 分布差异越大的结果越是我们需要的 query

    • p 和 q 的顺序和论文中的不同 $D(p \| q)=\sum_{x} p(x) \log \frac{p(x)}{q(x)}=E_{p(x)}\left(\log \frac{p(x)}{q(x)}\right)$

  • $K L(q \| p)=\ln \sum_{l=1}^{L_k} e^{q_i k_l^T / \sqrt{d}}-\frac{1}{L_k} \sum_{j=1}^L q_i k_j^T / \sqrt{d}-\ln L_k$

    • 把公式代入，然后化解

+ $M\left(q_i, K\right)=\ln \sum_{l=1}^{L_k} e^{q_i k_l^T / \sqrt{d}}-\frac{1}{L_k} \sum_{j=1}^{L_k} q_i k_j^T / \sqrt{d}$

  + 第一项是经典难题 log-sum-exp(LSE) 问题

  + 稀疏性度量 $M\left(q_i, K\right)$

    + $\ln L \leq M\left(q_i, K\right) \leq \max _j\left\{\frac{q_i k_j^T}{\sqrt{d}}\right\}-\frac{1}{L} \sum_{j=1}^L\left\{\frac{q_i k_j^T}{\sqrt{d}}\right\}+\ln L$

    + LSE 项用最大值来替代，即用和当前 qi 最近的 kj，所以才有下面取 top N 操作

      + $\bar{M}\left(\mathbf{q}_i, \mathbf{K}\right)=\max _j\left\{\frac{\mathbf{q}_i \mathbf{k}_j^{\top}}{\sqrt{d}}\right\}-\frac{1}{L_K} \sum_{j=1}^{L_K} \frac{\mathbf{q}_i \mathbf{k}_j^{\top}}{\sqrt{d}}$

+ $\mathcal{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{Softmax}\left(\frac{\overline{\mathbf{Q}} \mathbf{K}^{\top}}{\sqrt{d}}\right) \mathbf{V}$

  + $\bar{Q}$ 是稀疏矩阵，前 u 个有值

+ 具体流程

  + 为每个 query 都随机采样 N 个 key，默认值是 5lnL

    + 利用点积结果服从长尾分布的假设，计算每个  query 稀疏性得分时，只需要和采样出的部分 key 计算

  + 计算每个 query 的稀疏性得分

  + 选择稀疏性分数最高的 N 个 query，N 默认值是 5lnL

  + 只计算 N 个 query 和所有 key 的点积结果，进而得到 attention 结果

  + 其余 L-N 个 query 不计算，直接将 self-attention 层输入取均值(mean(V))作为输出

    + 除了选中的 N 个query index 对应位置上的输出不同，其他 L-N 个 embedding 都是相同的。所以新的结果存在一部分冗余信息，也是下一步可以使用 maxpooling 的原因

    + 保证每个 ProbSparse self-attention 层的输入和输出序列长度都是 L

+ 将时间和空间复杂度降为 $$O(L_K \log L_Q)$$

+ 如何解决 对于 multi-head self-attention 每个 head 都采用相同的优化策略

现象？

  + 每个 query 随机采样 key 这一步每个 head 的采样结果是相同的

  + 每一层 self-attention 都会先对 QKV 做线性转换，序列中同一个位置不同 head 对应的 query、key 向量不同

  + 最终每个 head 中得到的 N 个稀疏性最高的 query 也是不同的，相当于每个 head 都采取不同的优化策略

Self-attention distilling

• 突出 dominating score，缩短每一层输入的长度，降低空间复杂度到 $\mathcal{O}((2-\epsilon) L \log L)$

• encoder 层数加深，序列中每个位置的输出已经包含序列中其他元素的信息，所以可以缩短输入序列的长度

  • 过 attention 层后，大部分位置值相同

• 激活函数 [[ELU]]

• 通过 Conv1d + max-pooling layer 缩短序列长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class ConvLayer(nn.Module):
    def __init__(self, c_in):
        super(ConvLayer, self).__init__()
        self.downConv = nn.Conv1d(in_channels=c_in,
                                  out_channels=c_in,
                                  kernel_size=3,
                                  padding=2,
                                  padding_mode='circular')
        self.norm = nn.BatchNorm1d(c_in)
        self.activation = nn.ELU()
        self.maxPool = nn.MaxPool1d(kernel_size=3, stride=2, padding=1)

    def forward(self, x):
        x = self.downConv(x.permute(0, 2, 1))
        x = self.norm(x)
        x = self.activation(x)
        x = self.maxPool(x)
        x = x.transpose(1,2)
        return x

Generative style decoder

• 预测阶段通过一次前向得到全部预测结果，避免 dynamic decoding

• 不论训练还是预测，Decoder 的输入序列分成两部分 $X_{feed dcoder} = concat(X_{token}, X_{placeholder})$

  • 预测时间点前一段已知序列作为 start token

  • 待预测序列的 placeholder 序列

• 经过 deocder 后，每个 placeholder 都有一个向量，然后输入到一个全链接层得到预测结果

• 为什么用 generative style decoder #card

  • 解码器能捕捉任意位置输出和长序列依赖关系

  • 避免累积误差

Experiment

• Baseline

  • [[ARIMA]] [[Prophet]] [[DeepAR]]

  • [[Reformer]] dynamic decoding

• 实验设计

  • Univariate Time-series Forecasting

  • Multivariate Time-series Forecasting

    • LSTnet 是基线模型

  • Ablation Study

Input representation

• 提供时序信息

• 不是天级别更新的模型需要 global time stamp

  • week，month，holiday embedding

• 额外实验

  • 利用 t0-t1 的特征预测 t2-t3 结果还不错

  • 可能是 local time stamp 和 global time stamp 让 informer 不依赖自回归结果还能有不错的预测结果

See Also

• [[Informer/Code]]

• [[Informer/Question]]

Ref

• Informer: 一个基于Transformer的效率优化的长时间序列预测模型 - 知乎 (zhihu.com)

核心贡献

• Temporal Fusion Transformer 框架 #card

  • recurrent layers for local processing
    ls-type:: annotation
    hl-page:: 1
    hl-color:: yellow

  • interpretable self-attention layers for long-term dependencie
    ls-type:: annotation
    hl-page:: 1
    hl-color:: yellow

  • specialized components to select relevant features
    ls-type:: annotation
    hl-page:: 1
    hl-color:: yellow

  • a series of gating layers to suppress unnecessary components
    ls-type:: annotation
    hl-page:: 1
    hl-color:: yellow

• 模型可解释性 interpretable insights into temporal dynamics
  ls-type:: annotation
  hl-page:: 1
  hl-color:: yellow
  #card

  • 区分全局重要特征 globally-important variables for the prediction problem
    ls-type:: annotation
    hl-page:: 3
    hl-color:: yellow

  • 持久的时间模式 persistent temporal patterns
    ls-type:: annotation
    hl-page:: 3
    hl-color:: yellow

  • 显著事件 significant events
    ls-type:: annotation
    hl-page:: 3
    hl-color:: yellow

核心问题

• #card [[Multi-horizon Forecasting]] 包含复杂的输入特征组合 contains a complex mix of inputs
  ls-type:: annotation
  hl-page:: 1
  hl-color:: green

  • 静态变量

    • 与时间无关的静态变量 including static (i.e. time-invariant) covariates
      ls-type:: annotation
      hl-page:: 1
      hl-color:: green

  • 时变变量 Time-dependent Inputs

    • 已知未来输入 known future inputs,
      ls-type:: annotation
      hl-page:: 1
      hl-color:: green

      • 未来节假日信息

    • 外生时间序列 exogenous time series that are only observed in the past – without any prior information on how they interact with the target.
      ls-type:: annotation
      hl-page:: 1
      hl-color:: green

      • 历史顾客流量 historical customer foot traffic
        ls-type:: annotation
        hl-page:: 2
        hl-color:: green

  • 相关示意图

    • [:span]
      ls-type:: annotation
      hl-page:: 2
      hl-color:: yellow

• 使用 attention 机制增强 :-> 选择过去相关特征 used attention-based methods to enhance the selection of relevant time steps in the past
  ls-type:: annotation
  hl-page:: 2
  hl-color:: yellow

• 之前基于 DNN 方法的缺陷 #card

  • 没有考虑不同类型输入特征 fail to consider the different types of inputs
    ls-type:: annotation
    hl-page:: 2
    hl-color:: blue

    • 万物皆时序 构建模型时，将所有的特征按 time step 直接 concat 在一起，所有变量全部扩展到所有的时间步，无论是静态、动态的变量都合并在一起送入模型。

  • 假定所有外生输入都已知与未来 assume that all exogenous inputs are known into the future
    ls-type:: annotation
    hl-page:: 2
    hl-color:: blue

  • 忽略重要的静态协变量 neglect important static covariates
    ls-type:: annotation
    hl-page:: 2
    hl-color:: blue

    • 通常处理方法是预测时和其他时间相关特征连接

• 已有深度学习方法是黑箱，如何解释模型的预测结果？#card

  • do not shed light on how they use the full range of inputs present in practical scenarios
    ls-type:: annotation
    hl-page:: 1
    hl-color:: blue

相关工作

• [[@A Multi-Horizon Quantile Recurrent Forecaster]] Multi-horizon Quantile Recurrent Forecaster MQRNN 结构，同时预测未来多个时间步的值

• deep state space 状态空间模型，统计学，hybrid network，类似工作 [[ESRNN]] [[N-BEATS]]

• [[Explainable AI]]

  • post-hoc methods 事后方法（因果方法），不考虑输入特征的时间顺序 do not consider the time ordering of input features
    ls-type:: annotation
    hl-page:: 3
    hl-color:: blue

    • [[LIME]]

    • [[SHAP]]

  • 基于 attention 的架构对语言或语音序列有很好的解释，但是很难适用于多维度预测 attention-based architectures are proposed with inherent interpretability for sequential data
    ls-type:: annotation
    hl-page:: 3
    hl-color:: blue

解决方法

• [[Multi-horizon Forecasting]]

  • prediction intervals [[区间预测]] #card

    • [[DeepAR]] 直接修改模型的输出，模型不拟合原始标签，而是拟合人工指定的分布，通过蒙特卡洛采样取平均得到最终的点预测。

  • 分位数回归 [[Quantile Regression]]，每一个 time step 输出 $10^{th}$ $50^{th}$ $90^{th}$ #card

    • 不同分位数下预测能够产生预测区间，通过区间大小反应预测结果的不确定性。某个点在不同分位数线性回归的预测结果很接近，则预测确定性搞。

    • Quantile Outputs

    • $\hat{y}_i(q, t, \tau)=f_q\left(\tau, y_{i, t-k: t}, \boldsymbol{z}_{i, t-k: t}, \boldsymbol{x}_{i, t-k: t+\tau}, \boldsymbol{s}_i\right)$

    • 设计 [[quantile loss]]

      • $\begin{gathered}\mathcal{L}(\Omega, \boldsymbol{W})=\sum_{y_t \in \Omega} \sum_{q \in \mathcal{Q}} \sum_{\tau=1}^{\tau_{\max }} \frac{Q L\left(y_t, \hat{y}(q, t-\tau, \tau), q\right)}{M \tau_{\max }} \end{gathered}$

        • $Q L(y, \hat{y}, q)=q(y-\hat{y})_{+}+(1-q)(\hat{y}-y)_{+}$ #card

          • q 代表分位数

          • $(*)_+ = \max (0,*)$

          • 假设拟合分位数 0.9

          + $Q L(y, \hat{y}, q=0.9)=\max (0.9 *(y-\hat{y}), 0.1 *(\hat{y}-y))$

          + $y-\hat{y} \gt 0$ 模型预测偏小，Loss 增加更多

          + loss 中权重 9:1，模型倾向预测出大的数字，Loss 下降快

        + 假设拟合分位数 0.5，退化成 MAE

          + $Q L(y, \hat{y}, q=0.5)=\max (0.5 *(y-\hat{y}), 0.5 *(\hat{y}-y)) = 0.5*|y-\hat{y}|$

+ q-Risk 避免不同预测点下的预测量纲不一致问题，对结果做正则化处理。目前只关注 P50 和 P90 两个分位数 #card
  + $q$-Risk $=\frac{2 \sum_{y_t \in \tilde{\Omega}} \sum_{\tau=1}^{\tau_{\max }} Q L\left(y_t, \hat{y}(q, t-\tau, \tau), q\right)}{\sum_{y_t \in \tilde{\Omega}} \sum_{\tau=1}^{\tau_{\max }}\left|y_t\right|}$

• 模型结构 #card

  • [:span]
    ls-type:: annotation
    hl-page:: 6
    hl-color:: yellow

• 输入部分

  • [[Static Covariate Encoders]] 通过 GRN 将静态特征编码变成 4 个不同向量

  • 动态特征 #card

    • post inputs

    • known future inputs

  • [[Variable Selection Networks]] 通过选择重要的特征，减少不必要的噪音输入，以提供模型性能。 #card

    • [[GLU]] 灵感来自 LSTM 的门控机制，sigmoid 取值范围 0-1

  • 对不同类型的输入变量应该区别对待 #card

    • 静态变量通过特殊的 [[Static Covariate Encoders]]，后续做为 encoder 和 decoder 的输入

    • 过去的动态时变变量+动态时不变变量进入 encoder 结构中（蓝色 variable seletcion）

    • 未来的动态时不变变量进入 decoder 结构中

  • seq2seq with teacher forcing 架构 #card

    • encoder 部分动态特征 embedding 和静态特征 embedding concat 在一起做为输入

      • 静态变量 + 动态时变变量

    • decoder

      • 静态变量 + 动态时不变变量

• 模型组成

  • [[Gated Residual Network]] 模型能够灵活地仅在需要时应用非线性处理 #card

    • 外生输入和目标之间的确切关系通常是事先未知的，因此很难预见那些变量是相关的。

    • 很难确定非线性处理的程度该多大，并且可能存在更简单的模型就能满足需求。

  • [[Interpretable Multi-Head Attention]]

  • [[Temporal Fusion Decoder]] 学习数据集中的时间关系

  • 通过 dense 层得到多个 [[Quantile Outputs]] #card

    • $\hat{y}(q, t, \tau)=\boldsymbol{W}_q \tilde{\boldsymbol{\psi}}(t, \tau)+b_q$

[[TFT Interpretability Use Cases]] #card

• 输入特征重要性 examining the importance of each input variable in prediction
  ls-type:: annotation
  hl-page:: 17
  hl-color:: yellow

• 可视化当前时间模式 visualizing persistent temporal patterns
  ls-type:: annotation
  hl-page:: 17
  hl-color:: yellow

• 识别导致任何导致时间动态显著变化的时间 identifying any regimes or events that lead to significant changes in temporal dynamics
  ls-type:: annotation
  hl-page:: 17
  hl-color:: yellow

[[Ref]]

• [[@A Multi-Horizon Quantile Recurrent Forecaster]]

• temporal fusion transformer - 知乎 (zhihu.com)

• 关于tft的实现和细节 - 知乎 (zhihu.com)

• 时间序列|Temporal Fusion Transformer - 知乎 (zhihu.com)