DONE BERT 可解释性-从"头"说起 - 知乎 [[BERT]]，不停的 mask 结构，判断对指标的影响。[[2021/06/16]]

• 任务：query-title

  • 按 query-doc 相关程度分成 5 类

  • 用 BERT 做多分类

• 研究各个头对模型的影响：通过将 attention = 0 来 mask 对应的头

  • 12 层，每层 12 个 head，共 144 个 head

• 结论

  • attention-head 很冗余/鲁棒，去掉 20%的 head 模型不受影响

    • 144 个 head 随机 mask

    • 分成 0-5 层、6-11 层 mask

      • 底层特征对分类比较重要

  • 各层 transformer 之间不是串行关系，去掉一整层 attention-head 对下层影响不大

  • 各个 head 有固定的功能

    • 某些 head 负责分词

    • 某些 head 提取语序关系

    • 某些 head 负责提取 query-title 之间 term 匹配关系

[[香侬科技@为什么Transformer 需要进行 Multi-head Attention？]]

• 借鉴了CNN中同一卷积层内使用多个卷积核的思想

• Transformer，或Bert的特定层是有独特的功能的，底层更偏向于关注语法，顶层更偏向于关注语义。

• 多头中多数的关注模式是一致的

  • 不同的关注模式由初始化带来

• 就是希望每个注意力头，只关注最终输出序列中一个子空间，互相独立。其核心思想在于，抽取到更加丰富的特征信息。

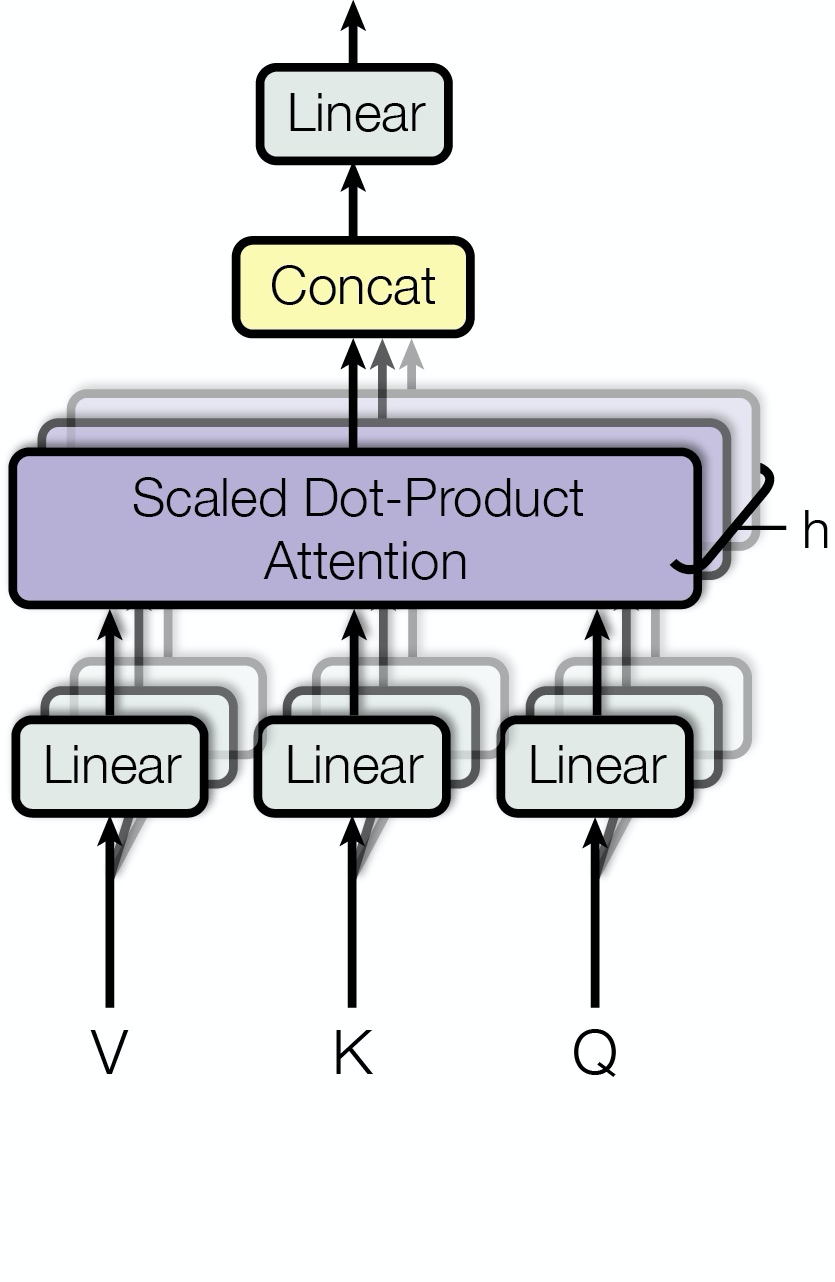
利用多组 $$W$$ 值和 $$X$$ 相乘，得到多组不同的 $$Q$$ $$K$$ $$V$$，分别利用这几组向量去做 self-attenttion，最终将得到的 attention 结果 concat 在一起。

$$\begin{aligned} \text { MultiHead }(Q, K, V) &=\text { Concat }\left(\text { head }_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head }_{\mathrm{i}} &=\operatorname{Attention}\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned}$$

$$W_{i}^{Q} \in \mathbb{R}^{d_{\text { model }} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{\text { model }} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{\text { model }} \times d_{v}}$$

论文中每一层有 h=8 个 attention

输入的向量大小为 512，为了保持大小相同，每个 attention 中的 $$d_k=d_v=d_{model}/h=64$$

从原理上来看，multi-head 相当于在计算次数不变的情况下，将整个 attention 空间拆成多个 attention 子空间，引入了跟多的非线性从而增强模型的表达能力。

论文中一共使用了三种 multi-head attention

• encoder-decoder attention：query 来自前一个 decoder 层的输出，keys,values 来自最后一个 encoder 输出。

  • 其意义是： decoder 的每个位置去查询它与 encoder 的哪些位置相关，并用 encoder 的这些位置的 value 来表示。

• encoder self-attention：query,key,value 都来自前一层 encoder 的输出。这允许 encoder 的每个位置关注 encoder 前一层的所有位置。

• decoder masked self-attention：query,key,value 都来自前一层 decoder 的输出。这允许 decoder 的每个位置关注 encoder 前一层的、在该位置之前的所有位置。

• 第一种 QVV 模式，后面两种 VVV 模式

RNN 为了解决不定长输入，LSTM 的三个门结构为了解决标准 RNN 的梯度爆炸和长序列信息消失问题

硅谷谷主

• [[self-attention]] 用句子中有所单词向量的加权和来代表某一个单词的向量。

Transformer 缺乏时间维度建模，通过 [[Positional Encoding]] 也和 LSTM 这种天然的时序网络有差距。

• 缺乏时间维度建模导致深层 Transformer 编码器的每个位置输出都会很相似(每一层不断在上一层的基础上加权和)

Transformer 效果表现好建立在预训练的基础上，单独训练 Transformer 需要大量技巧

• 编码器层数，attention head 数量，学习率，权重衰减

香港中文大学曾爱玲文章，在长时间序列预测问题上使用线性模型打败基于 Transformer 的模型，并对已有模型的能力进行实验分析（灵魂7问，强烈推荐好好读一下！）。

[[Abstract]]

• Transformers have achieved superior performances in many tasks in natural language processing and computer vision, which also triggered great interests in the time series community.

• Among multiple advantages of transformers, the ability to capture long-range dependencies and interactions is especially attractive for time series modeling, leading to exciting progress in various time series applications.

  • In this paper, we systematically review transformer schemes for time series modeling by highlighting their strengths as well as limitations. In particular, we examine the development of time series transformers in two perspectives.

    • From the perspective of network structure, we summarize the adaptations and modification that have been made to transformer in order to accommodate the challenges in time series analysis.

    • From the perspective of applications, we categorize time series transformers based on common tasks including forecasting, anomaly detection, and classification.

  • Empirically, we perform robust analysis, model size analysis, and seasonal-trend decomposition analysis to study how transformers perform in time series.

  • Finally, we discuss and suggest future directions to provide useful research guidance.

• A corresponding resource list which will be continuously updated can be found in the GitHub repository1.

[[Attachments]]

• Transformers in Time Series-2022.pdf

Input Encoding and Positional Encoding

• Absolute Positional Encoding

• Relative Positional Encoding

• Hybrid positional encodings

Network Modifications for Time Series

• [[Positional Encoding]]

  • Vanilla Positional Encoding

  • Learnable Positional Encoding

    • [[A transformer-based framework for multivariate time series representation learning]] introduce an embedding layer in Transformer that learn embedding vectors for each position index jointly with other model parameters.

    • [[Temporal Fusion Transformers]] 使用 LSTM 对位置进行编码，更好适应时序预测任务

  • Timestamp Encoding

    • calendar timestamps(hours, minute…) 和 special timestamps (holidays and events)

    • [[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting]] [[Autoformer]] [[FEDformer]] 将 timestamps 特征转换成 embedding 通过网络学习

    • 如何生成好的 timestamp encoding 比较依赖人工先验

• Attention Module

  • 提升 self-attention 计算效率

  + [[LogTrans]] [ Li et al., 2019 ] and [\[\[Pyraformer\]\]](/post/logseq/%40Pyraformer%3A%20Low-Complexity%20Pyramidal%20Attention%20for%20Long-Range%20Time%20Series%20Modeling%20and%20Forecasting.html) explicitly introducing a sparsity bias

  + 移除 self-attention 矩阵部分值 [\[\[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting\]\]](/post/logseq/%40Informer%3A%20Beyond%20Efficient%20Transformer%20for%20Long%20Sequence%20Time-Series%20Forecasting.html) [[FEDformer]]

• Architecture Level

  • renovate transformer

  • hierarchical architecture 分层结构

    • 针对考虑到时间序列的多分辨率(多周期，多趋势叠加)

      • [[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting]] max-pooling layer

      • [[Pyraformer]] C-ary tree base attention mechanism

        • nodes at the finest scale correspond to the original time series

        • nodes in the coarser scales represent series at lower resolutions

        • both intra-scale and inter-scale attentions in order to better capture temporal dependencies across different resolutions

Applications of Time Series Transformers

• Forecasting

  • Time Series Forecasting

    • [[LogTrans]]

      • proposed convolutional self-attention by employing causal convolutions to generate queries and keys in the self-attention layer 因果卷积引入子注意力计算

      • a Logsparse mask

    • [[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting]]

    • AST [[Adversarial sparse transformer for time series forecasting]]

      • 使用生成对抗编码器-解码器架训练用于时间序列预测的稀疏 Transformer 模型

      • 对抗训练可以直接塑造网络的输出来改善预测效果，避免逐步预测带来的累积误差

        • directly shaping the output distribution of network to avoid the error accumulation through one-step ahead inference

    • [[Autoformer]]

      • simple seasonaltrend decomposition architecture 简单季节性趋势分解架构

      • an auto-correlation mechanism working as an attention module 自相关机制注意力模块 $O(L\log L)$

        • measures the time-delay similarity between inputs signal and aggregate the top-k similar sub-series to produce the output

    • [[FEDformer]]

      • 利用 [[Fourier transform]] 和 [[Wavelet transform]] 处理 frequency domain 频域中的注意力操作

        • linear complexity

    • [[@Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting]]

      • multi-horizon forecasting model with static covariate encoders, gating feature selection and temporal self-attention decoder

    • [[SSDNet]] [[ProTran]]

      • combine Transformer with state space models to provide probabilistic forecasts 提供概率预测

    • [[Pyraformer]]

      • hierarchical pyramidal attention module with binary tree following path

      • 分层金字塔注意力模块，二叉树

    • [[Aliformer]]

      • Knowledge-guided attention

  • Spatio-Temporal Forecasting [[Traffic Flow Forecasting]]

    • Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting

      • self attention module to capture temporal-temporal dependencies 时序特征

      • Graph neural network module to capture spatial dependencies 空间特征

    • Spatialtemporal Transformer

      • 空间 transformer 辅助图卷积网络来捕获空间依赖关系

    • Spatio-temporal graph Transformer

      • 基于注意力的图卷积机制

  • Event Forecasting

    • temporal point processes (TPP)

• Anomaly Detection

• Classification

  • [[GTN]]

Experimental Evaluation and Discussion

模型鲁棒性、模型大小以及对时序季节性和趋势捕捉能力

• robustness analysis, model size analysis, and

seasonal-trend decomposition analysis

• seasonal-trend decomposition 是 transformer 解决时序预测的重要组成部分

• 所有模型加上 moving average trend decomposition architecture proposed 结构后，和原始模型相比效果都获得提升

Future Research Opportunities

• [[inductive bias]] for Time Series Transformers

  • 避免过拟合，训练 transformer 需要大量数据。

  • 时序数据具有 seasonal/periodic and trend patterns

  • 将对于时序数据模型的理解和特定任务的特征做为归纳偏置引入 transformer

• [[GNN]]

  • 增强对于空间依赖和多维度之间的关系建模能力

• [[预训练]]

  • 目前针对时间序列的预训练 transformer 集中在时序分类任务中

• [[Neural architecture search]]

  • 如果构建高效的 transformer 结构

Ref

• TODO [[A transformer-based framework for multivariate time series representation learning]]

• TODO [[Adversarial sparse transformer for time series forecasting]]

• DONE [[@Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting]]
  completed:: [[2022/11/08]]

• TODO [[SSDNet]]

• TODO [[ProTran]]

• [[LogSparse Transformer]]

• Transformer应用于时序任务的综述【2022by阿里达摩院】 - 知乎 (zhihu.com)

  • 影响预测效果的细节

    • 训练

    • Encoder 间的特征工程

[[Abstract]]

• Many real-world applications require the prediction of long sequence time-series, such as electricity consumption planning. Long sequence time-series forecasting (LSTF) demands a high prediction capacity of the model, which is the ability to capture precise long-range dependency coupling between output and input efficiently. Recent studies have shown the potential of Transformer to increase the prediction capacity. However, there are several severe issues with Transformer that prevent it from being directly applicable to LSTF, including quadratic time complexity, high memory usage, and inherent limitation of the encoder-decoder architecture. To address these issues, we design an efficient transformer-based model for LSTF, named Informer, with three distinctive characteristics: (i) a ProbSparse self-attention mechanism, which achieves O(L log L) in time complexity and memory usage, and has comparable performance on sequences’ dependency alignment. (ii) the self-attention distilling highlights dominating attention by halving cascading layer input, and efficiently handles extreme long input sequences. (iii) the generative style decoder, while conceptually simple, predicts the long time-series sequences at one forward operation rather than a step-by-step way, which drastically improves the inference speed of long-sequence predictions. Extensive experiments on four large-scale datasets demonstrate that Informer significantly outperforms existing methods and provides a new solution to the LSTF problem.

[[Attachments]]

• Informer_2021_Zhou.pdf

Long sequence [[Time Series Forecasting]] (LSTF)

• 长序列时间序列预测需要模型能够有效捕捉输出和输入之间精确的 long-range dependency coupling

LSTF 中使用 [[Transformer]] 需要解决的问题 #card #incremental

• self-attention 计算复杂度 $O(L^2)$

• 多层 encoder/decoder 结构内存增长

• dynamic decoding 方式预测耗时长

网络结构

ProbSparse self-attention

• 替换 inner product self-attention

  • [[Sparse Transformer]] 结合行输入和列输出

  • [[LogSparse Transformer]] cyclical pattern

  • [[Reformer]] locally-sensitive hashing(LSH) self-attention

  • [[Linformer]]

  • [[Transformer-XL]] [[Compressive Transformer]] use auxiliary hidden states to capture long-range dependency

  • [[Longformer]]

• 其他优化 self-attention 工作存在的问题

  • 缺少理论分析

  • 对于 multi-head self-attention 每个 head 都采用相同的优化策略

• self-attention 点积结果服从 long tail distribution

  • 较少点积对贡献绝大部分的注意力得分

  • 现实含义：序列中某个元素一般只会和少数几个元素具有较高的相似性/关联性

• 第 i 个 query 用 $q_i$ 表示

  • $\mathcal{A}\left(q_i, K, V\right)=\sum_j \frac{f\left(q_i, k_j\right)}{\sum_l f\left(q_i, k_l\right)} v_j=\mathbb{E}_{p\left(k_j \mid q_i\right)}\left[v_j\right]$

  • $p\left(k_j \mid q_i\right)=\frac{k\left(q_i, k_j\right)}{\sum_l f\left(q_i, k_l\right)}$

  • $k\left(q_i, k_j\right)=\exp \left(\frac{q_i k_j^T}{\sqrt{d}}\right)$

• query 稀疏性判断方法

  • $p(k_j|q_j)$ 和[[均匀分布]] q 的 [[KL Divergence]]

    • q 是均分分布，相等于每个 key 的概率都是 $\frac{1}{L}$

    • 如果 query 得到的分布类似于均匀分布，每个概率值都趋近于 $\frac{1}{L}$，值很小，这样的 query 不会提供什么价值。

    • p 和 q 分布差异越大的结果越是我们需要的 query

    • p 和 q 的顺序和论文中的不同 $D(p \| q)=\sum_{x} p(x) \log \frac{p(x)}{q(x)}=E_{p(x)}\left(\log \frac{p(x)}{q(x)}\right)$

  • $K L(q \| p)=\ln \sum_{l=1}^{L_k} e^{q_i k_l^T / \sqrt{d}}-\frac{1}{L_k} \sum_{j=1}^L q_i k_j^T / \sqrt{d}-\ln L_k$

    • 把公式代入，然后化解

+ $M\left(q_i, K\right)=\ln \sum_{l=1}^{L_k} e^{q_i k_l^T / \sqrt{d}}-\frac{1}{L_k} \sum_{j=1}^{L_k} q_i k_j^T / \sqrt{d}$

  + 第一项是经典难题 log-sum-exp(LSE) 问题

  + 稀疏性度量 $M\left(q_i, K\right)$

    + $\ln L \leq M\left(q_i, K\right) \leq \max _j\left\{\frac{q_i k_j^T}{\sqrt{d}}\right\}-\frac{1}{L} \sum_{j=1}^L\left\{\frac{q_i k_j^T}{\sqrt{d}}\right\}+\ln L$

    + LSE 项用最大值来替代，即用和当前 qi 最近的 kj，所以才有下面取 top N 操作

      + $\bar{M}\left(\mathbf{q}_i, \mathbf{K}\right)=\max _j\left\{\frac{\mathbf{q}_i \mathbf{k}_j^{\top}}{\sqrt{d}}\right\}-\frac{1}{L_K} \sum_{j=1}^{L_K} \frac{\mathbf{q}_i \mathbf{k}_j^{\top}}{\sqrt{d}}$

+ $\mathcal{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{Softmax}\left(\frac{\overline{\mathbf{Q}} \mathbf{K}^{\top}}{\sqrt{d}}\right) \mathbf{V}$

  + $\bar{Q}$ 是稀疏矩阵，前 u 个有值

+ 具体流程

  + 为每个 query 都随机采样 N 个 key，默认值是 5lnL

    + 利用点积结果服从长尾分布的假设，计算每个  query 稀疏性得分时，只需要和采样出的部分 key 计算

  + 计算每个 query 的稀疏性得分

  + 选择稀疏性分数最高的 N 个 query，N 默认值是 5lnL

  + 只计算 N 个 query 和所有 key 的点积结果，进而得到 attention 结果

  + 其余 L-N 个 query 不计算，直接将 self-attention 层输入取均值(mean(V))作为输出

    + 除了选中的 N 个query index 对应位置上的输出不同，其他 L-N 个 embedding 都是相同的。所以新的结果存在一部分冗余信息，也是下一步可以使用 maxpooling 的原因

    + 保证每个 ProbSparse self-attention 层的输入和输出序列长度都是 L

+ 将时间和空间复杂度降为 $$O(L_K \log L_Q)$$

+ 如何解决 对于 multi-head self-attention 每个 head 都采用相同的优化策略

现象？

  + 每个 query 随机采样 key 这一步每个 head 的采样结果是相同的

  + 每一层 self-attention 都会先对 QKV 做线性转换，序列中同一个位置不同 head 对应的 query、key 向量不同

  + 最终每个 head 中得到的 N 个稀疏性最高的 query 也是不同的，相当于每个 head 都采取不同的优化策略

Self-attention distilling

• 突出 dominating score，缩短每一层输入的长度，降低空间复杂度到 $\mathcal{O}((2-\epsilon) L \log L)$

• encoder 层数加深，序列中每个位置的输出已经包含序列中其他元素的信息，所以可以缩短输入序列的长度

  • 过 attention 层后，大部分位置值相同

• 激活函数 [[ELU]]

• 通过 Conv1d + max-pooling layer 缩短序列长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class ConvLayer(nn.Module):
    def __init__(self, c_in):
        super(ConvLayer, self).__init__()
        self.downConv = nn.Conv1d(in_channels=c_in,
                                  out_channels=c_in,
                                  kernel_size=3,
                                  padding=2,
                                  padding_mode='circular')
        self.norm = nn.BatchNorm1d(c_in)
        self.activation = nn.ELU()
        self.maxPool = nn.MaxPool1d(kernel_size=3, stride=2, padding=1)

    def forward(self, x):
        x = self.downConv(x.permute(0, 2, 1))
        x = self.norm(x)
        x = self.activation(x)
        x = self.maxPool(x)
        x = x.transpose(1,2)
        return x

Generative style decoder

• 预测阶段通过一次前向得到全部预测结果，避免 dynamic decoding

• 不论训练还是预测，Decoder 的输入序列分成两部分 $X_{feed dcoder} = concat(X_{token}, X_{placeholder})$

  • 预测时间点前一段已知序列作为 start token

  • 待预测序列的 placeholder 序列

• 经过 deocder 后，每个 placeholder 都有一个向量，然后输入到一个全链接层得到预测结果

• 为什么用 generative style decoder #card

  • 解码器能捕捉任意位置输出和长序列依赖关系

  • 避免累积误差

Experiment

• Baseline

  • [[ARIMA]] [[Prophet]] [[DeepAR]]

  • [[Reformer]] dynamic decoding

• 实验设计

  • Univariate Time-series Forecasting

  • Multivariate Time-series Forecasting

    • LSTnet 是基线模型

  • Ablation Study

Input representation

• 提供时序信息

• 不是天级别更新的模型需要 global time stamp

  • week，month，holiday embedding

• 额外实验

  • 利用 t0-t1 的特征预测 t2-t3 结果还不错

  • 可能是 local time stamp 和 global time stamp 让 informer 不依赖自回归结果还能有不错的预测结果

See Also

• [[Informer/Code]]

• [[Informer/Question]]

Ref

• Informer: 一个基于Transformer的效率优化的长时间序列预测模型 - 知乎 (zhihu.com)