自动特征交叉，解决特征稀疏

FM 与其他模型对比

• 可以模拟二阶多项式核的 [[SVM]]、MF、SVD++

  • [[SVM]] 训练和预测需要计算核矩阵，核矩阵的复杂度是 N 方

  • MF 扩展性没有 FM 好，只有 u 和 i 两类特征

与 [[SVM]] 对比

• 二阶多项式内核 SVM 二元交叉特征 wij 相互独立

  • fm 参数 nk，svm 参数 nn，更适合大规模稀疏特征，泛化能力更强

• 核方法需要计算核矩阵

• 样本 :-> FM 预测和训练样本独立，SVM 和支持向量有关

• FM 在原始形式下 进行优化学习，非线性SVM通常需要在 对偶形式 下进行
  交叉项需不需要乘 value ？

• eta 放到 xi 和 xj 泛化能力不好

FM 如何加入 index embedding？

对比 FM 和 SVM 有什么区别？

• 特征角度 :-> 二阶多项式内核 SVM 二元交叉特征 wij 相互独立
  ， ((6302f9ee-11be-4f7a-9cf9-26400d6d4601))
  为什么要用 FTRL 优化 FM #card

• FTRL 是 SGD 算法，离线调参，减少线上风险

• 稀疏特征， 自适应学习率效果最好(特征 i 在 t 轮迭代的学习率不同)

• 不同特征有不同的学习速度、收敛速度快

[[Ref]]

• 深入FFM原理与实践 - 美团技术团队

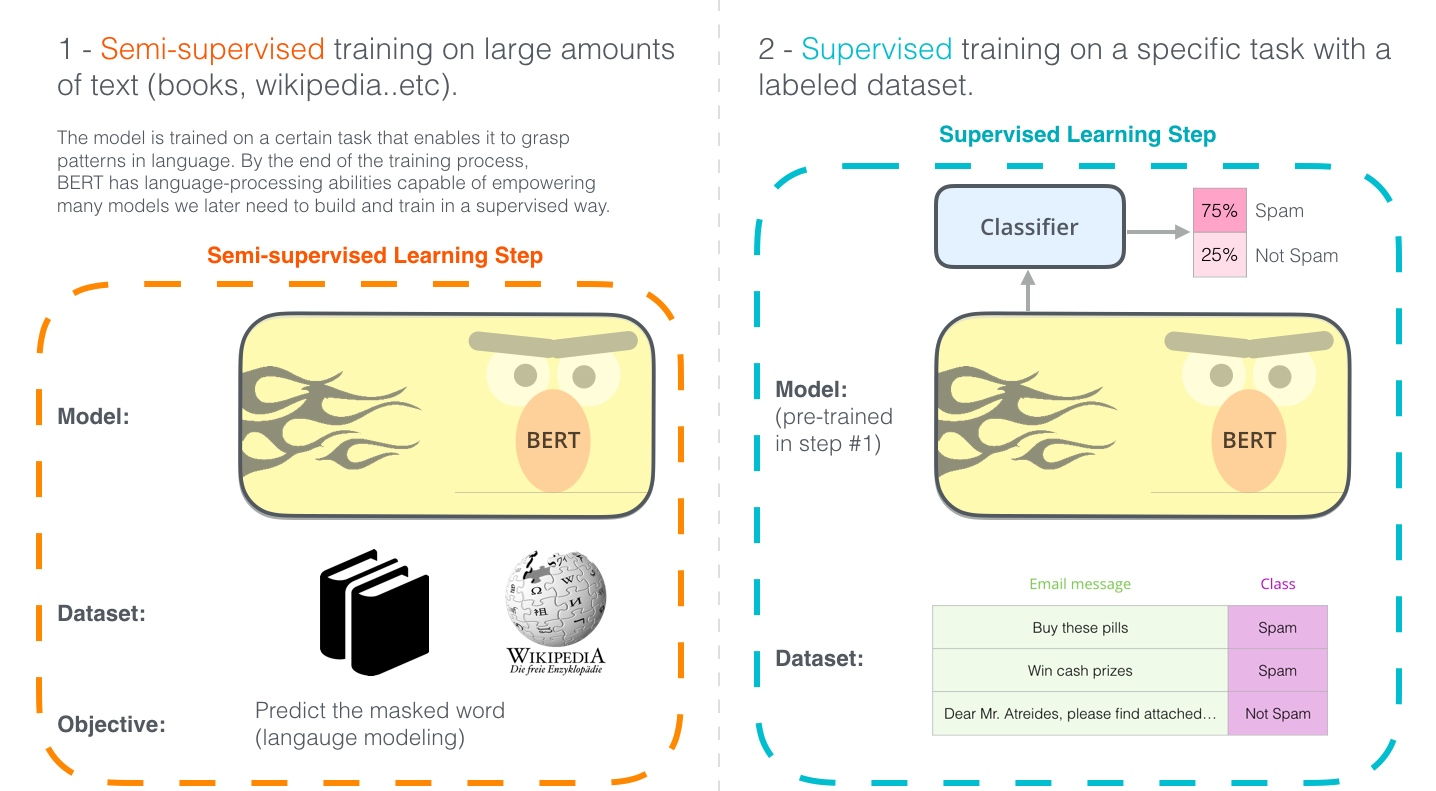
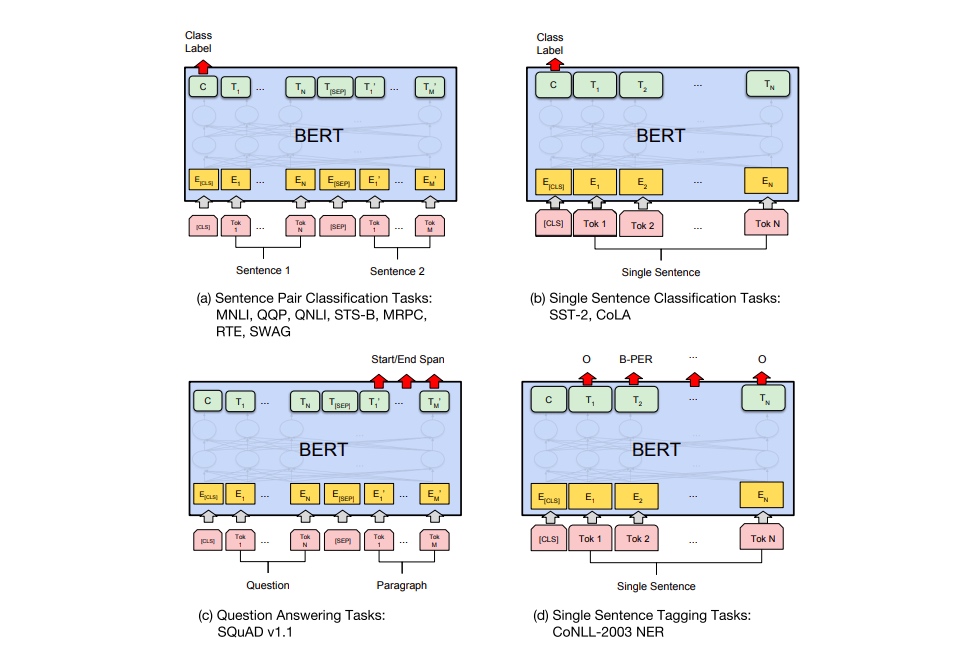
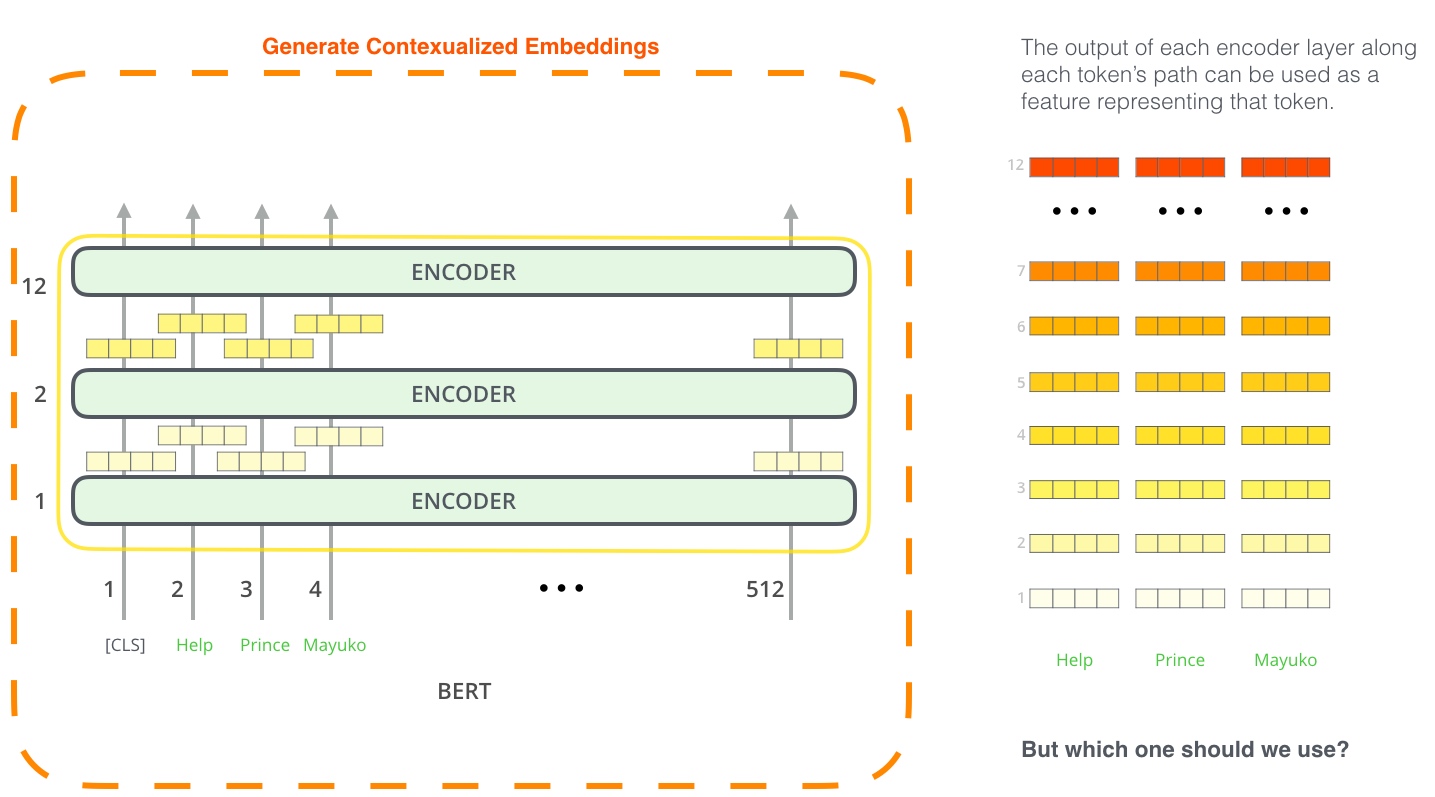
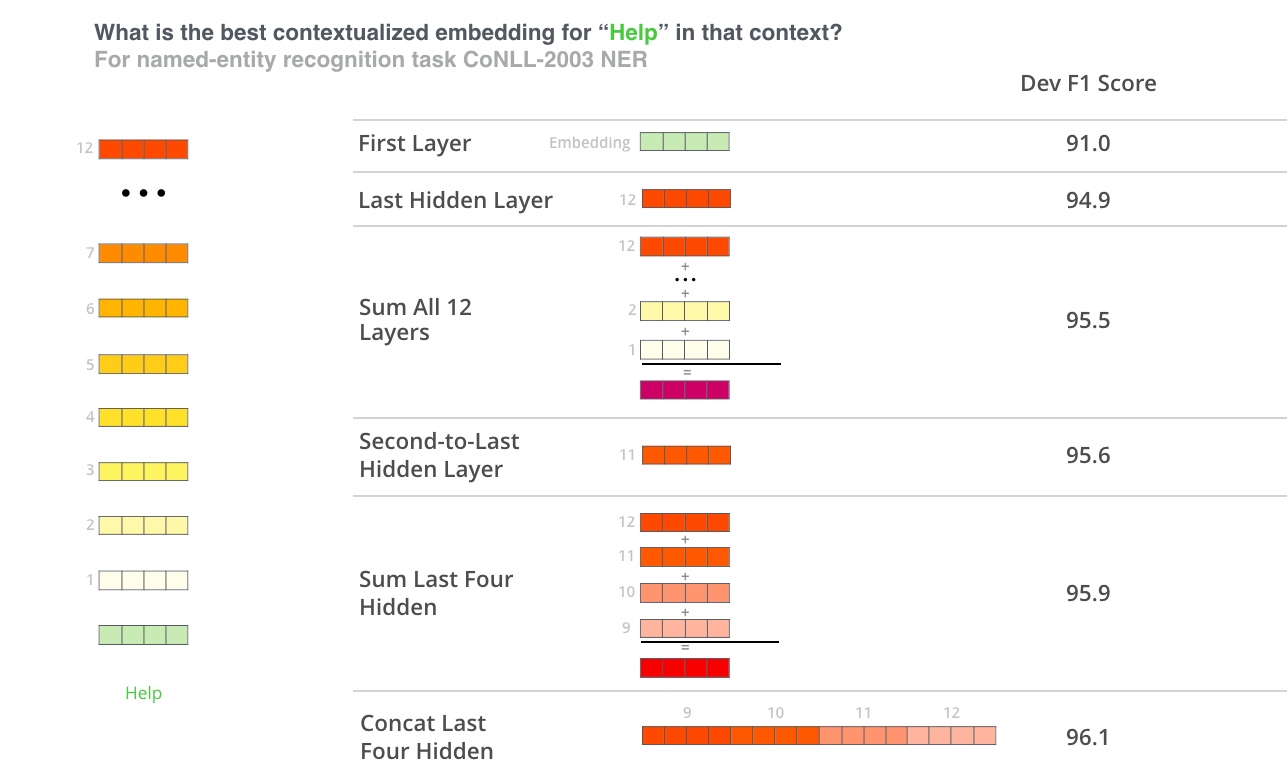
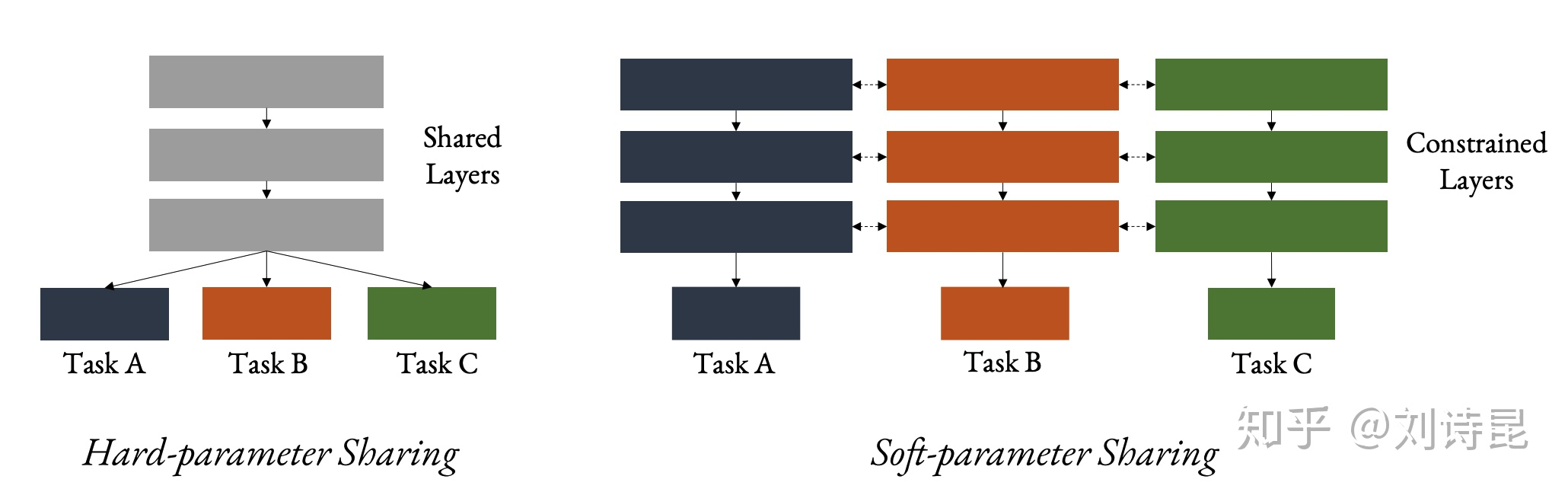
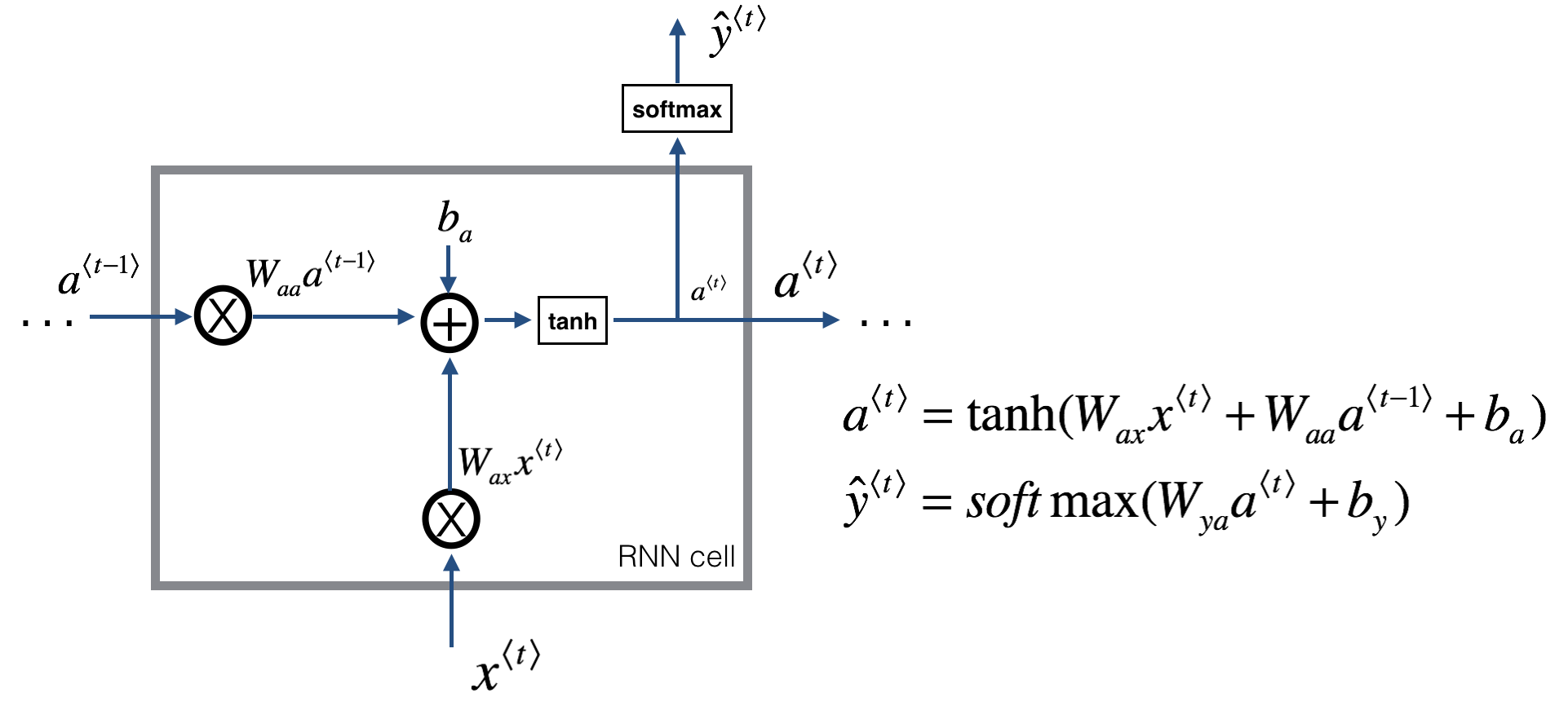
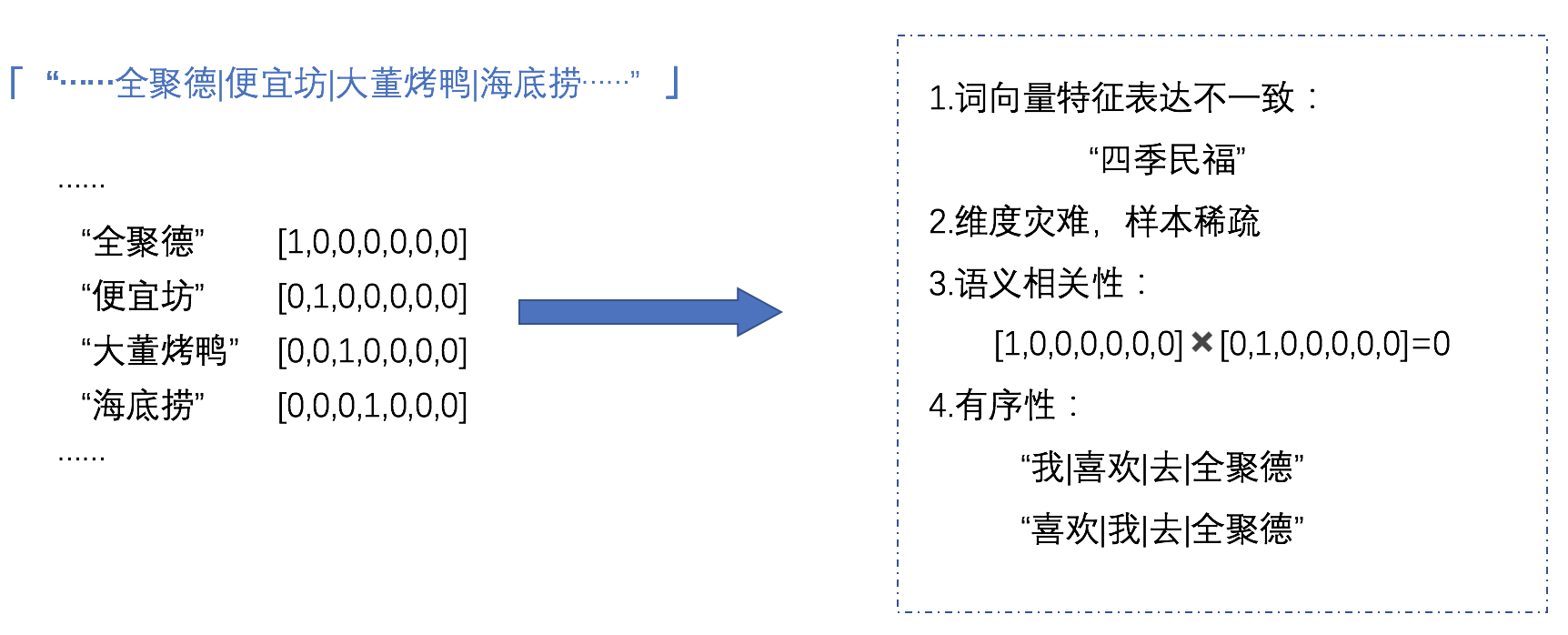
[[PTM]] pre-train-model

17 年 Google 发表论文 「Attention is all you need」提出 Transformers 框架，之后一大批人在此基础上进行研究和应用。原始 Transformer 改进的变体被称为 「X-formers」。

X-formers 改进方向有三个：

• Model Efficiency

  • self-attetion 带来的计算量和参数量(内存)

    • sparse attention 轻量级注意力机制方案

    • divide-and-conquer methods 分治方法

• Model Generalization

  • 框架灵活，对数据没有太多的结构偏置

  • 训练需要数据量大

  • structural bias or regularization, pre-training on large-scale unlabeled data

• Model Adaptation

  • 将 Transformer 应用到具体的下游任务中。

背景知识

• 见 [[Transformer]]

模型使用形式

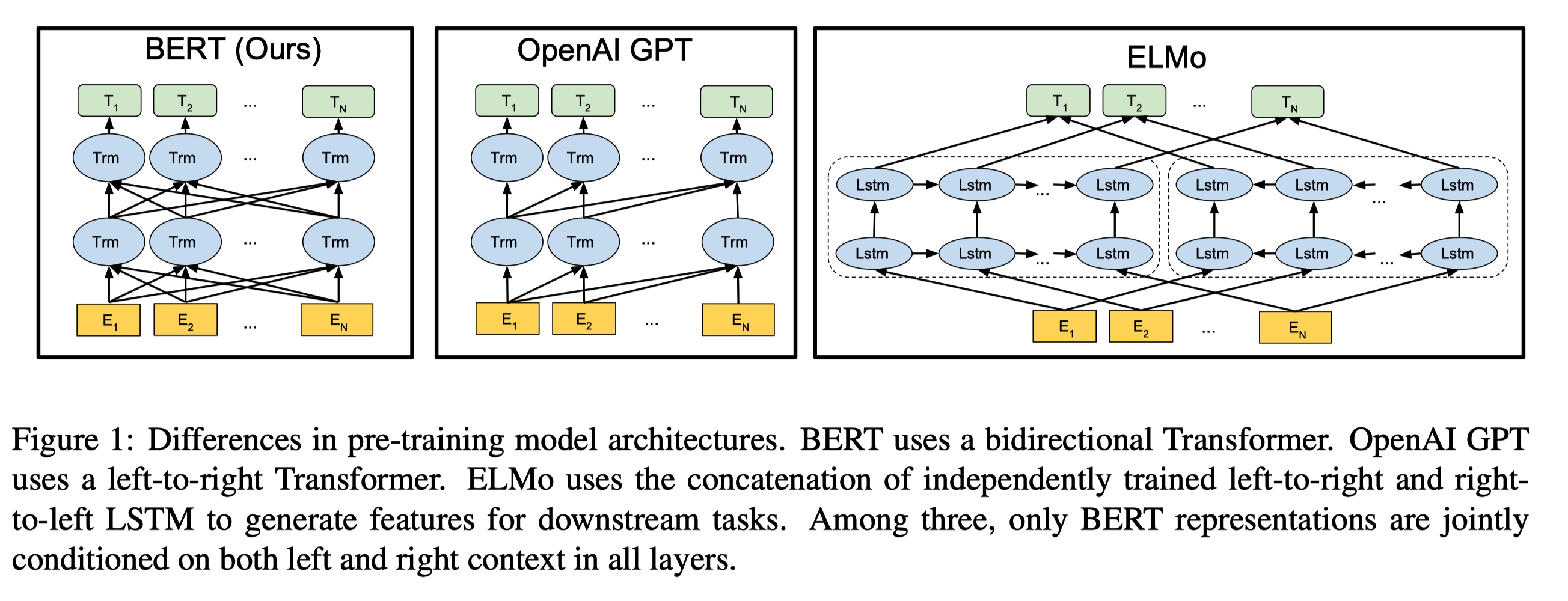
• Encoder-Decoder

• Encoder only

  • classification or sequence labeling

• Decoder only

  • sequence generation

    • language modeling

根据对原始 Transformer 的改进分类：architecture modification, pre-training, and applications

• architecture modification

  • Module Level

    • [[Attention]]

      • 挑战

        • 计算复杂度，受序列长度影响

        • Structural prior 没有结构先验，在小数据集上容易过拟合

      • Sparse Attention

        • token i 和 j 有关系的情况下计算 attention，以稀疏矩阵形式保存

        • 如何定义关系

          • position-based

            • 计算指定位置之间的 attention

            • atomic sparse attention

              • Global

              • Band

              • Dilated

            • 组合 atomic attention 得到更加复杂的attention计算规则

          • content-based

            • Routing Transformer

              • Efficient Content-Based Sparse Attention with RoutingTransformers

              • 聚类

            • [[Reformer]]

              • 使用 LSH，同一个分桶内的 token 计算 attention

      • [[Linearized Attention]]

        • QKV 计算 Attention 的复杂度是 $$O(T^2D)$$，通过引入核函数降低到 $$O(TD)$$

        • key components

          • kernel feature map

            • Performer 用其他函数去拟合 attention 函数

              • FAVOR+ Fast Attention Via positive Orthogonal Random features approach

          • aggregation rule

      • Query Prototyping and Memory Compression

        • 减少 queries or key-value pairs

        • Query Prototyping 计算关键 query 的 attention 值，剩余部分填充或者采用均匀分布填充

          • [[@Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting]]

        • Memory Compression 减少 kv 数量

      • Low-rank Self-Attention

        • attention 矩阵线性相关的行数 A 远小于输入 T

        • Low-rank Parameterization

        • Low-rank Approximation

      • Attention with Prior

        • 分成 generated attention 和 prior attention 两部分，下面的方法都是生成 prior attention 尝试

        • Prior that Models locality

          • 文本之类的数据对位置敏感，使用 i 和 j 的位置，结合[[Normal Distribution]]计算先验信息

        • Prior from Lower Modules

          • 使用之前层的注意力分布结果

          • Realformer 将 [[ResNet]] 结构放到 Attention 矩阵中

          • Lazyformer 每两层计算一次 Attention 矩阵

        • Prior as Multi-task Adapters

          • 多任务适配器，看起来是在共享参数

        • Attention with Only Prior

          • 只使用先验

      • Improved Multi-Head Mechanism

        • Head Behavior Modeling

        • Multi-head with Restricted Spans

          • 观察到原始中部分 head 关注局部，部分关注全局

          • 限制 attention 的范围(通过距离实现)

          • decoder 中 mask-multi-head 就是这个思路

        • Multi-head with Refined Aggregation

          • 多头的结果如何合并

          • routing methods

        • Other Modifications

          • Shazeer multi-query attention 所有头之间共享 kv

          • Bhojanapalli 灵活设置 head size

    • OTHER MODULE-LEVEL MODIFICATIONS

      • Position Representations

        • Transformer 具有排列不变性，需要而外位置信息

        • Absolute Position Representations

          • 正余弦编码

          • 位置向量

        • Relative Position Representations.

          • token 之间的关系更加重要

          • 将 embedding 加到 key 的attention中

          • Transformer-XL

        • Other Representations

          • TUPE

            • 混合相对和绝对位置

          • Roformer

            • 旋转位置编码

            • 线性 attention 中实现相对位置编码

          • Position Representations without Explicit Encoding 不要编码

            • R-Transformer 先过 RNN 再将输出结果输入到多头

            • CPE 使用卷积

          • Position Representation on Transformer Decoders

            • 移除 pe

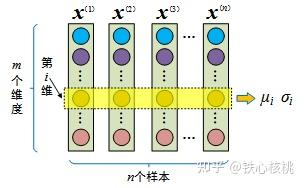
      • LayerNorm

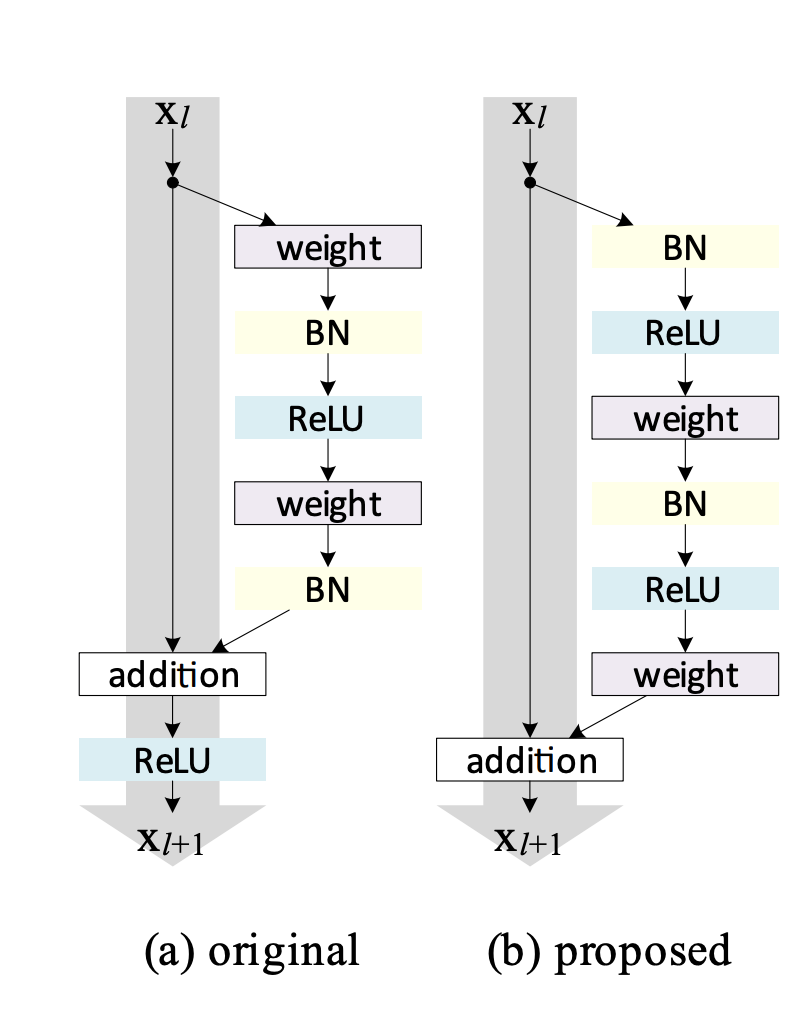
        • Placement of Layer Normalization

          • post-LN

          • pre-LN 保证 skip 链接路上没有其他操作

        • Substitutes of Layer Normalization

          • 可学习参数效果不好，

          • AdaNorm

          • scaled l2 normalization

          • PowerNorm

        • Normalization-free Transformer

          • ReZero 可学习残差模块替代 LN

      • FFN

        • Activation Function in FFN

          • [[Swish]]

          • [[GPT]] [[GELU]]

        • Adapting FFN for Larger Capacity

          • product-key memory layers

          • MoE

            • 取 top k 专家

            • 取最大专家

            • 分组取各自 top1

        • Dropping FFN Layers

          • 简化网络

  • Arch. Level

    • Adapting Transformer to Be Lightweight

      • Lite Transformer

      • Funnel Transformer

        • hidden sequence pooling and up-sampling

      • DeLighT

        • DeLighT block

    • Strengthening Cross-Block Connectivity

      • 针对 decoder 解决问题

      • Transparent Attention

      • Feedback Transformer

        • 使用前一步所有层的信息

    • [[Adaptive Computation Time]]

      • 解决之前模型中层数固定

      • 三种方法

        • [[Universal Transformers]]dynamic halting

          • 达到停止条件的 token 不再改变

        • CCT

          • 跳层

    • Transformers with Divide-and-Conquer Strategies

      • 将 LM 任务中长文本拆分成多个片段

      • Recurrent Transformers 上一个 T 输出信息输入到下一个输入

        • Transformer-XL 上一个输出和下一个输入 concat 在一起

      • Hierarchical Transformers 多个结果聚合

        • Hierarchical for long sequence inputs

          • sentence Transformer and document Transformer

        • Hierarchical for richer representations 更丰富的表示

          • 字母级别表示和词级别表示

    • Exploring Alternative Architecture

      • NAS

  • PRE-TRAINED TRANSFORMERS

    • Encoder only

      • [[BERT]]

    • Decoder only

  • APPLICATIONS OF TRANSFORMER

    • CV

      • [[ViT]]

  • CONCLUSION AND FUTURE DIRECTIONS

    • 理论分析

    • 更好全局交互机制

    • 处理多种类数据的框架

[[Layer Normalization]]

$c_{i}=\sum_{j=1}^{T_{x}} \alpha_{i j} h_{j}$

• $\alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{T_{x}} \exp \left(e_{i k}\right)}$ 是隐藏状态 $h_j$ 的权重

  • 用 softmax 得到一个强度表征

  • 为什么需要使用 softmax 做归一化 #card #incremental

    • 避免 attention score 数值过大，导致优化不稳定(数值小的部分)

    • 保证 score 非负

$e_{i j}=a\left(s_{i-1}, h_{j}\right)$ 是注意力打分机制

• 代表 :-> 解码器状态 $s_{i-1}$ 和解码器状态 $h_j$ 之间的匹配程度

• 常用的注意力计算方式

  • 加性模型 :-> $s \left(\mathbf{x}_{i}, \mathbf{q}\right) =\mathbf{v}^{\mathrm{T}} \tanh \left(W \mathbf{x}_{i}+U \mathbf{q}\right)$
    • qkv 矩阵较大时效果超越 dot production
  • 点积模型 :-> $s\left(\mathbf{x}_{i}, \mathbf{q}\right) =\mathbf{x}_{i}^{\mathrm{T}} \mathbf{q}$
    • 不需要额外参数，但是两个矩阵大小需相同
  • 缩放点积模型 :-> $s\left(\mathbf{x}_{i}, \mathbf{q}\right) =\frac{\mathbf{x}_{i}^{\mathrm{T}} \mathbf{q}}{\sqrt{d}}$
  • 双线性模型 :-> $s\left(\mathbf{x}_{i}, \mathbf{q}\right) =\mathbf{x}_{i}^{\mathrm{T}} W \mathbf{q}$
    聚焦式（focus）注意力：

• 自上而下的有意识的注意力，主动注意——是指有预定目的、依赖任务的、主动有意识地聚焦于某一对象的注意力。

$$\text{ Attention (Query, Source) }=\sum_{i=1}^{L_{x}} \text{ Similarity (Query, Key}_{i} ) * \text{Value}_{i}$$

流程可视化

为什么要用 attention

• 参数少，速度快，能缓解神经网络模型复杂度。解决 RNN 不能并行计算问题

• 效果显著

按计算区域划分

• soft-attention(global attention) :-> query 对所有 key 求相似度权重，得到 m*n 的 attention score
  

  • $\begin{aligned} \operatorname{att}((K, V), \mathbf{q}) &=\sum_{i=1}^{N} \alpha_{i} \mathbf{v}_{i} \\ &=\sum_{i=1}^{N} \frac{\exp \left(s\left(\mathbf{k}_{i}, \mathbf{q}\right)\right)}{\sum_{j} \exp \left(s\left(\mathbf{k}_{j}, \mathbf{q}\right)\right)} \mathbf{v}_{i} \end{aligned}$

• hard-attention :-> 直接精准定位到某个 key，其余的 key 不管，单个样本 query 仅对单个 key 进行相似度计算，得到 m*1 的 attention score

• local-attention :-> hard定位单个key，以这个 key 为中心取周围区域，计算各个窗口的 soft-attention，得到 m*k 的 attention score
  按所用信息

• general-attention :-> 利用外部信息，用于构建两段文本之间关系的任务

• [[self-attention]] :-> 只使用内部信息，寻找原文内部的关系。
  按使用模型

• CNN 是基于 N-gram 的局部编码，RNN 由于梯度消失问题也只能建立短距离依赖。

• 解决上面的问题有两种方法：利用深层神经网络来获取远距离的信息交互或者是使用全连接网络。

• [[LSTM]] 对所有 step 的 hidden state 进行加权，注意力集中到整段文本中比较重要的 hidden state 信息。

[[Attention 按 QKV 划分]]

注意力计算方式 Neural Machine Translation by Jointly Learning to Align and Translate

Ref

• transformer中为什么使用不同的K 和 Q， 为什么不能使用同一个值？ - 知乎 (zhihu.com)
• TODO Dissecting BERT Part 1: The Encoder | by Miguel Romero Calvo | Dissecting BERT | Medium 看 softmax 相关的计算

[[@BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding]]

代码：google-research/bert: TensorFlow code and pre-trained models for BERT

大模型 + 微调提升小任务的效果

输入层

• 词嵌入（token embedding）、位置嵌入（position embedding）段嵌入（segment embedding）

  • 预训练任务包含判断 segment A 和 segment B 之间的关系

• 模型结构 12 层，每层 12 个 multi-head

• CLS 句子开头，最后的输出 emb 对应整句信息

  • 无语义信息的符号会更公平地融合文本中各个词的语义信息，从而更好的表示整句话的语义

• SEP 句子之间分割

BERT

• L=12 H=768 A=12, Total Parameters=110M

• L=24 H=1024 A=16, Total Parameters=340M

两种 NLP 预训练

• 1. 产出产品，例如 word2evc 的 embedding
• 2. 做为骨架接新结构

[[ELMo]]

• 使用 LSTM 预测下一个单词

[[GPT]]

• Transformer

• 单向

贡献性

• 双向信息重要性

模型输入：

• 1. Token emb
• 2. Segment emb(A B) 针对 QA 或者两个句子的任务
• 3. Position emb

训练方式

• [[Masked-Language Modeling]] :->mask 部分单词，80 % mask，10 % 错误单词， 10% 正确单词

  • 目的 :-> 训练模型记忆句子之间的关系。
    • 减轻预训练和 fine-tune 目标不一致给模型带来的影响

• [[Next Sentence Prediction]] :-> 预测是不是下一个句子

  • 句子 A 和句子 B 有 50% 的概率是上下文

  • 解决后续什么问题 :-> QA 和自然语言推理
    
    occlusion:: eyIuLi9hc3NldHMvaW1hZ2VfMTczNDYxNjMzODQyMV8wLnBuZyI6eyJjb25maWciOnt9LCJlbGVtZW50cyI6W3sibGVmdCI6MzY3LjEzMDExNTk3NDg1MjYsInRvcCI6NTkuNDE3NTUwMDkwNDM3Mzk1LCJ3aWR0aCI6NjIzLjU5MTg3MjM5Mzc2MDksImhlaWdodCI6MTE4LjgzNTEwMDE4MDg3NDc2LCJhbmdsZSI6MCwiY0lkIjoxfSx7ImxlZnQiOjEwODEuOTAzNDAxNTY2MDE5LCJ0b3AiOjY1LjA2OTA2NDM1NDU0MTcsIndpZHRoIjo2NjUuMjAzOTI0MjY0NDI2LCJoZWlnaHQiOjkwLjM5NTU1NzkzMTAxMTA3LCJhbmdsZSI6MCwiY0lkIjoyfV19fQ==
    [[激活函数]] [[GELU]]

• 和 [[GPT]] 一致，为什么？

优化器

• 不完整版 adam

• fine tune 时可能不稳定，需要换成正常版 adam

fine tune

• 根据任务调整输入和增加预测结构，使用相关数据训练

• 使用 fine tune 比将bert做为特征放到模型中效果要好

• 1. 双句分类
• 2. 单句分类
  • CLS 后接 softmax
• 3. 预测一个 start 和 end embedding，然后和 T 计算 softmax 取概率最大的做为开始和结束的位置
• 4. 实体标注

研究取不同的 embedding 效果

缺陷

• 不擅长生成类任务(机器翻译、文本摘要)

[[Ref]]

• [[Multimodal BERT]]

• The Illustrated BERT, ELMo, and co. (How NLP Cracked Transfer Learning) – Jay Alammar – Visualizing machine learning one concept at a time

• 如何评价 BERT 模型？ - 知乎

• NLP 从语言模型看Bert的善变与GPT的坚守 - 知乎

  • 像Bert这样的双向语言模型为何要做 masked LM？[[GPT]] 为何一直坚持单向语言模型？ Elmo 也号称双向，为何不需要 mask？[[Word2Vec]] 的 CBOW 为何也不用 mask？

  • indirectly see themselves

  • GPT 保留用上文生成下文的能力

• 为什么 Bert 的三个 Embedding 可以进行相加？ - 知乎

  • 三个 embedding 相加和拼接

    • 联系 :-> 三个 embedding 相加相当于三个原始的 one-hot 拼接再经过一个全连接网络。
      • 优点 :-> 和拼接相比，相加可以节约模型参数。
      • 实验显示拼接并没有相加效果好，拼接后维度增加，需要再经过一个线性变换降低维度，增加了更多参数。

  • 之前的理解和多个波长不同的波相加，最后还是能分离出来，所以模型也应该能区分。

  • 空间维度很高，模型能区分各个组分

    • 参数空间量 30k2512

    • 模型表达能力至少是 2^768

  • 梯度角度，(f + g +h)' = f' + g' + h'

• BERT—容易被忽视的细节

  • 细节三：对于任务一，对于在数据中随机选择 15% 的标记，其中80%被换位[mask]，10%不变、10%随机替换其他单词，原因是什么？#card

    • [mask] 在 fine-tune 任务中不会出现，模型不知道如何处理。

    • 缓解上面的现象

    • 15% 标记被预测，需要更多训练步骤来收敛

缓解神经网络“内部协方差漂移”（[[Internal Covariance Shift]], ICS）

• How Does Batch Normalization Help Optimization?

对每个隐藏层输入进行 0-1 标准化

神经网络本身是为了学习数据的分布，如果训练集和测试集分布不同，会导致学习的神经网络泛化性能大大降低

• 每一层神经网络依赖前一层神经网络，如果前一层分布一直改变，后一层很学习。

网络每次迭代需要拟合不通的数据分布，增大训练的复杂度以及过拟合的风险。

对输入的数据分布进行额外的约束，从而增强模型的泛化能力，但也降低了模型的拟合能力

[[covariate shift]] 源空间和目标空间的条件概率是一致的，但是其边缘概率不同。神经网络的各层输出由于层内操作，其分布显然与各层对应的输入信号分布不同。

在神经网络训练时遇到收敛速度很慢，或者梯度爆炸等无法训练时可以尝试使用。

batch_mean, bacth_var = tf.nn.moments(data, [0]) 求 data 数据的每一列的均值和方差

tf.nn.batch_normalization(data, mean, variance, offset, scale, variance_epsilon, name=None)

• offset 和 scale 是参数，分别初始化为 0 和 1
• variance_epsilon 很小的一个值，防止除零
  批归一化也会降低模型的拟合能力，比如 sigmoid 激活函数中，批量归一化后数据整体处于函数的非饱和区，破坏之前学到的连接权重。引入 offset 和 scala 是为了能还原成最初的输入，与之前的网络层解耦。

$\mu_{i}=\frac{1}{M} \sum x_{i}, \quad \sigma_{i}=\sqrt{\frac{1}{M} \sum\left(x_{i}-\mu_{i}\right)^{2}+\epsilon}$

• 对每个维度的特征计算均值和标准差

算法流程

occlusion:: eyIuLi9hc3NldHMvaW1hZ2VfMTcyNDE3MjAzMTgxN18wLnBuZyI6eyJjb25maWciOnsiaGlkZUFsbFRlc3RPbmUiOnRydWV9LCJlbGVtZW50cyI6W3sibGVmdCI6MTkxLjUxNTUyOTA3NzA4ODUzLCJ0b3AiOjE4OS41OTQ0MTY2NTQ0MjUyMywid2lkdGgiOjEzMS4xMTE5ODc5MjE3NDAxNCwiaGVpZ2h0IjoxMTEuMDQ2MzYzNjc5NTEyNjQsImFuZ2xlIjowLCJjSWQiOjF9LHsibGVmdCI6MjM3LjYyNjk0ODU1ODAzOTU0LCJ0b3AiOjI5My41MjM4MzU2MzQwMjc1Mywid2lkdGgiOjIyNS41NTcwNjM5NjcwNjExNywiaGVpZ2h0Ijo4OS43NDU0MTY3MDE4ODkyMSwiYW5nbGUiOjAsImNJZCI6Mn0seyJsZWZ0IjoyNDguMTgyNTc0NzA0MjgxMywidG9wIjozODEuOTEwMzMxMTI3MTkxMzQsIndpZHRoIjoyNDIuMjIzODQyMDkyNzA2MTUsImhlaWdodCI6NzUuMTAwMTE2Njg3NjUwMDcsImFuZ2xlIjowLCJjSWQiOjN9LHsibGVmdCI6MjY2LjUxNjAzMDY0MjQ5MDcsInRvcCI6NDUxLjA3ODgwMTY1ODU3NzEsIndpZHRoIjoyNzguODkwNzUzOTY5MTI0OTQsImhlaWdodCI6NTguOTE0MTUzMDI3MTIyODksImFuZ2xlIjowLCJjSWQiOjR9LHsibGVmdCI6NjAzLjY0ODM4NDc1Njg5NTQsInRvcCI6MTk1LjAyMjI3MzI2Mjk1NTIsIndpZHRoIjoxOTcuOTYzMzQ3MDEzMjc0NTYsImhlaWdodCI6NTQuNDEyOTk1NjA2OTAwNjQsImFuZ2xlIjowLCJjSWQiOjV9LHsibGVmdCI6NTg3LjkyNzU4NTQ5NDI5NTQsInRvcCI6MjkzLjg0NDM0ODI0MTY1MzcsIndpZHRoIjoyMzYuMDcxNjU2Nzg4NzMyNTUsImhlaWdodCI6NDUuNTQ4NjI2MzI2NTA1NzcsImFuZ2xlIjowLCJjSWQiOjZ9LHsibGVmdCI6NjI3LjUzNjE2NDM5MTM4MDgsInRvcCI6MzczLjczOTY1NTI2MDY1MzU0LCJ3aWR0aCI6MTU4LjQsImhlaWdodCI6NDMuNDQ0NjUyNjE4NzA3ODM1LCJhbmdsZSI6MCwiY0lkIjo3fSx7ImxlZnQiOjYxOS40MjY5ODM2MTU4MTI5LCJ0b3AiOjQ0NC41MzkyOTM0MTA5MDQyNCwid2lkdGgiOjE3NS4yOTUwOTc2MjkxMTY5OCwiaGVpZ2h0Ijo0My45ODU0NDY0NzUwMDc5NiwiYW5nbGUiOjAsImNJZCI6OH1dfX0=
原理

• 1. 加快网络训练和收敛的速度：每层数据的分布一致
• 2. 防止梯度爆炸和梯度消失
• 3. BN 防止过拟合：minibatch 中的样本被关联在一起，一个样本的输出取决于样本本身，也取决于同属一个batch的其他样本。

[[Batch Normalization/前向和反向传播]]

[[Batch Normalization/维度理解]]

如何得到预测时 BN 层使用的均值和方差？

• 1. 训练时，保留每组 mini-batch 训练数据在网络每一层的均值和方差
  • 均值、方差是基于所有批次的期望计算所得
    • $E[x] \leftarrow E_{B}\left[\mu_{B}\right]$
    • $\operatorname{Var}[x] \leftarrow \frac{m}{m-1} E_{B}\left[\sigma_{B}^{2}\right]$
• 2. moving statistics [[Batch Normalization/Moving average]]

  • 如果训练时使用这个方法，会减少当前 batch 对参数的影响

  • Batch Normalization 训练的时候为什么不使用 moving statistics？ - 知乎 (zhihu.com)

    • 不能对统计量求导

    • 除以标准差后的梯度方向是与减均值之后的feature垂直的，用这个梯度更新不会引起 feature scale 的剧变，从而解决梯度爆炸

    • moving statistics 对于 BN输入的变化是滞后的

为什么BN层一般用在线性层和卷积层后面，而不是放在非线性单元后

• BN 层希望得到 0-1 高斯分布 的数据

• 非线性单元之后的数据分布 不一定对称

• 实践中 BN 放在 ReLU 后面 #card

  • Normalization 一般是在输入层之前对数据处理，Batch-Normalization 可以视作对传给隐藏层的输入的normalization。

• 放在 tanh 或 sigmoid 之前，可以 避免进入饱和区，缓解梯度衰减问题 。
  BN 和 [[ReLU]] 的顺序关系？

• [[ResNet]] :-> Skip -> BN -> RELU -> Conv -> BN -> RELU -> Conv -> Add

  • [[Identity Mappings in Deep Residual Networks]]

• BN-ReLU
  • 特点 :-> BN 后输入数据更接近 0 均值，或减轻数据落入负区间梯度消失现象，或更好展现 ReLU 的单侧抑制作用进行特征选择
• ReLU-BN
  • 特点 :-> 激活后再 Norm，保证下一层的输入是零均值的。
    [[Batch Normalization/多卡同步]]

[[Batch Normalization 为何有效]]

[[Ref]]

• https://app.yinxiang.com/shard/s67/nl/14454592/45035394-974f-4cf0-8796-e2fe30b478d0/

• Batch-normalized 应该放在非线性激活层的前面还是后面？ - 知乎

• BatchNormalization详解_Panda-CSDN博客_batchnormalization引用格式

[[NLP]] 中比较常用

参数 B 控制 beam width

翻译任务中：第一次选取概率最高的 B 个词语。第二次在这 B 个词语上进行扩展下一个单词，然后选取概率最高的 B 个词组，以此类推，直到结束。B=1 时相当于贪心。

在 [[Seq2Seq]] 中应用在 decode 部分

[[Transformer]] 解决实际预测环节如何构造一个理想输出

[[Ref]]

• Seq2Seq中的beam search算法 - 知乎

• seq2seq 中的 beam search 算法过程是怎样的？ - 知乎

指标

• CVR 转化率

  • SSB: Sample Selection Bias，训练时集合是点击的样本，正样本为转换的，负样本为未转化。预测时空间为全体样本，存在 bias

在 Wide & Deep 基础上，对 Wide 部分进行改进。LR 无法进行特征交叉，FM 受限于性能一般只去做二阶交叉，Cross 可以实现高阶交叉。DCN 和 DNN 相比，相同效果情况下可以减少参数量。

Cross 网络只能处理定长的输入，[[ETA]] v4 中无法使用……

特征处理和常规的模型一样，Sparse feature 经过 embedding 处理，然后和 Dense feature concat 在一起。由于 Cross network 每一层的大小都和输入向量大小相等，如果 Sparse feature 不处理，输入维度会很大，然后参数量会增加。

Cross 和 Deep 的输出结果 concat 后过一个 LR 直接输出。

Cross Network

• 每一层都是由 $x_0$ 和前一层的输出 $x_l$ 交叉学习残叉。

• ResNet 的引入可以将网络做的更深。

• 特点：有限高阶、自动叉乘、参数共享

• $$\mathbf{x}_{l+1}=\mathbf{x}_{0} \mathbf{x}_{l}^{T} \mathbf{w}_{l}+\mathbf{b}_{l}+\mathbf{x}_{l}=f\left(\mathbf{x}_{l}, \mathbf{w}_{l}, \mathbf{b}_{l}\right)+\mathbf{x}_{l}$$

• 图中可以看到随着层数的增加，参数 w 会线性增加。

Deep NetWork

• Cross Network 中的参数量太少，不能学习高维的非线性特征。

Analysis

• Cross 的设计最后包含了每个特征的从 1 阶到高阶的特征组合。与 FM 不同每个特征组合的参数部分共享，所以能降低参数量，比 FM 有更好的泛化性和鲁棒性。比如 FM 可以解决 xi 和 xj 没有同时出现过的情况，但是 Cross 能处理 xi 和 xj 都没有出现过的情况 ……

亮点

• 1. 引入辅助 Loss：利用 GRU 的 hidden state 与下一个点击的商品做一个
• 2. 一般模型把用户行为直接当成兴趣，dien 认为用户兴趣是隐藏在行为中，需要去挖掘

• feature 分成四类：User Profile, User Behavior, Ad and Context

• [[interest extractor layer]] 作用 :-> 兴趣抽取层，用 GRU 抽取序列信息

• [[interest evolving layer]] 作用 :-> 兴趣进化层，将Target Attention引入GRU，过滤掉与待排序的广告不相关的信息。

• [[AUGRU]] 计算方法 #card

  • 这里是先用序列中Item的隐状态和待排序的广告Embedding计算一个Attention标量，再将该标量乘以更新门控向量。

  • 最终隐藏状态和候选状态，以及每一个维度的重要性，由当前Item隐状态，待排序广告，前一Item隐状态，当前Item原特征（后两者用于计算更新门）共同决定。

源码阅读

• train.py 指定模型

• model 中包含对模型的实现

• 数据

  • uid_voc.pkl: 用户名对应的id

  • mid_voc.pkl: item对应的id

  • cat_voc.pkl:category对应的id

  • item-info:item对应的category信息

  • reviews-info：用于进行负采样的数据

  • local_train_splitByUser:训练数据，一行格式为：label、用户名、目标item、 目标item类别、历史item、历史item对应类别。

  • local_test_splitByUser:测试数据，格式同训练数据

• 网络设置

  • embeeding 18

  • hidden size 18＊2

  • attention_size 18*2

  • fcn: 200-80-2

  • dice

  • prelu

• 需要分析代码：

  • aux 网络

  • gru 改造

  • din_fcn_attention

[[Ref]]

• 详解阿里之Deep Interest Evolution Network(AAAI 2019) - 知乎

• Deep Interest and Evolution Network for CTR - 知乎

• 也评Deep Interest Evolution Network - 知乎

快速傅里叶变换 - OI Wiki (oi-wiki.org)

模型用来逼近 特征上限
[[特征设计原则四象限]]
[[特征设计]]

[[特征选择]]

• 特征值之间的方差小，代表其 识别能力较弱 。

[[数据清洗]] 对异常数据进行清洗，最常见的异常有空值异常（缺省值处理）、数值溢出（数值异常处理）。

[[特征变换]]

• [[类别特征]] 包括离散特征、id特征

• [[数值特征]]

• [[时间特征]] 数值和离散两种

• [[内容特征]]

• [[统计特征]]

使用方式

• 特征加权

  • [[SENET]]

  • [[Attention]]

  • [[CNN]]

• [[特征交叉]]

• [[Feature Hashing]]

• [[标签和权重如何使用？]]

• [[如何把相似的实体算作一类 one-hot ？]]

• [[类似 automl 的特征字典]]

特征重要性分析和[[特征选择]]

特征抽取

• 线性判别分析[[Fisher]]

• [[PCA]]

• [[自编码器]]

[[深度学习不需要特征工程？]]

Explicit Semantic Cross Feature Learning via Pre-trained Graph Neural Networks for CTR Prediction

• 使用 GNN 构造 (用户特征，物料特征) 的交叉特征

• 预估输入特征的 xtr

Ref

• @探讨特征工程的方法论

  • [[类似 automl 的特征字典]]

  • 基于业务逻辑去做特征工程

  • 特征重要性表的特征工程思路

    • 利用 xgb/lgb 输出特征重要性，对重要性高的特征交叉

    • 通过 embedding 对物品进行泛化

• 工业级推荐系统中的特征工程 - 知乎 (zhihu.com)

  • 误区

    • 深度学习不需要特征工程？

      • 模型可以学习 row-based 的特征变换，很难学习 column-based 特征变换(counting，tf-idf)

    • [[AutoML]] 工具取代特征工程？

    • 特征工程没有技术含量？

  • 搜广推场景下的特征工程

    • high-cardinality 属性表示位特征时的挑战

    • 对特征进行统计，分桶，然后再交叉

解决高斯分布的单峰性，引入多个高斯模型加权平均拟合数据

几何角度

• $$p(x)=\sum _{k=1}^{K} \alpha _k N( \mu _k, \Sigma _k), \sum \alpha = 1$$

生成模型角度

• 利用离散变量 z 来选择来自哪一个高斯分布

• $$p(x)=\sum\limits_zp(x,z)=\sum\limits_{k=1}^Kp(x,z=k)=\sum\limits_{k=1}^Kp(z=k)p(x|z=k)$$

• 得到 $$p(x)=\sum\limits_{k=1}^Kp_k\mathcal{N}(x|\mu_k,\Sigma_k)$$
  [[MLE]] 求解

• 求解上面的 px

• $$\theta_{MLE}=\mathop{argmax}\limits_{\theta}\log p(X)=\mathop{argmax}_{\theta}\sum\limits_{i=1}^N\log p(x_i)=\mathop{argmax}_\theta\sum\limits_{i=1}^N\log \sum\limits_{k=1}^Kp_k\mathcal{N}(x_i|\mu_k,\Sigma_k)$$

• log 中有连加号存在，无法求出解析解。
  [[EM]] 求解

• EM 目标求解：$\theta ^{(t+1)} = \arg \max _{\theta} \int _Z \log [p(X,Z|\theta)]p(Z|X, \theta ^{(t)})dZ = \arg \max _{\theta} E _{z|x,{\theta ^t}} [\log p(X,Z|\theta)]$

• E-Step

  • $$Q(\theta,\theta^t)=\sum\limits_z[\log\prod\limits_{i=1}^Np(x_i,z_i|\theta)]\prod \limits_{i=1}^Np(z_i|x_i,\theta^t)\\$$

+ 对第一个累加号展开，第一项为： + $$\sum\limits_z\log p(x_1,z_1|\theta)\prod\limits_{i=1}^Np(z_i|x_i,\theta^t)=\sum\limits_z\log p(x_1,z_1|\theta)p(z_1|x_1,\theta^t)\prod\limits_{i=2}^Np(z_i|x_i,\theta^t)\\ =\sum\limits_{z_1}\log p(x_1,z_1|\theta) p(z_1|x_1,\theta^t)\sum\limits_{z_2,\cdots,z_K}\prod\limits_{i=2}^Np(z_i|x_i,\theta^t)\\ =\sum\limits_{z_1}\log p(x_1,z_1|\theta)p(z_1|x_1,\theta^t)

  + 后面与 1 无关求和结果为1

+ $$Q(\theta,\theta^t)=\sum\limits_{i=1}^N\sum\limits_{z_i}\log p(x_i,z_i|\theta)p(z_i|x_i,\theta^t)$$

  + $$p(x,z|\theta)=p(z|\theta)p(x|z,\theta)=p_z\mathcal{N}(x|\mu_z,\Sigma_z)$$

  + $$p(z|x,\theta^t)=\frac{p(x,z|\theta^t)}{p(x|\theta^t)}=\frac{p_z^t\mathcal{N}(x|\mu_z^t,\Sigma_z^t)}{\sum\limits_kp_k^t\mathcal{N}(x|\mu_k^t,\Sigma_k^t)}$$

+ $$Q=\sum\limits_{i=1}^N\sum\limits_{z_i}\log p_{z_i}\mathcal{N(x_i|\mu_{z_i},\Sigma_{z_i})}\frac{p_{z_i}^t\mathcal{N}(x_i|\mu_{z_i}^t,\Sigma_{z_i}^t)}{\sum\limits_kp_k^t\mathcal{N}(x_i|\mu_k^t,\Sigma_k^t)}$$

• M-Step

  • $$Q=\sum\limits_{k=1}^K\sum\limits_{i=1}^N[\log p_k + \log \mathcal{N}(x_i|\mu_k,\Sigma_k)]p(z_i=k|x_i,\theta^t)$$

  • $$p_k^{t+1}=\mathop{argmax}_{p_k}\sum\limits_{k=1}^K\sum\limits_{i=1}^N[\log p_k+\log \mathcal{N}(x_i|\mu_k,\Sigma_k)]p(z_i=k|x_i,\theta^t)\ s.t.\ \sum\limits_{k=1}^Kp_k=1$$

    • 化简 $$p_k^{{t+1}=\mathop{argmax}_{p_k}\sum\limits_{k=1}}K\sum\limits_{i=1}^N\log p_kp(z_i=k|x_i,\theta^{t) s.t. \sum\limits_{k=1}}Kp_k=1$$

    • [[Lagrange Multiplier]] $$L(p_k,\lambda)=\sum\limits_{k=1}^{K\sum\limits_{i=1}}N\log p_kp(z_i=k|x_i,\theta^{t)-\lambda(1-\sum\limits_{k=1}}Kp_k)$$

    • [[Lagrange]] $$L(p_k,\lambda)=\sum\limits_{k=1}^{K\sum\limits_{i=1}}N\log p_kp(z_i=k|x_i,\theta^{t)-\lambda(1-\sum\limits_{k=1}}Kp_k)$$

    • $$\frac{\partial}{\partial p_k}L=\sum\limits_{i=1}^N\frac{1}{p_k}p(z_i=k|x_i,\theta^t)+\lambda=0\\$$

\Rightarrow\lambda=-N$$

  + $$p_k^{t+1}=\frac{1}{N}\sum\limits_{i=1}^Np(z_i=k|x_i,\theta^t)$$

+ $$\mu_k,\Sigma_k$$ 无约束参数，直接求导

对比 MLE 和 EM 在求解 GMM 问题上的区别

• $\theta_{MLE}=\mathop{argmax}\limits_{\theta}\log p(X)=\mathop{argmax}_{\theta}\sum\limits_{i=1}^N\log p(x_i)=\mathop{argmax}_\theta\sum\limits_{i=1}^N\log \sum\limits_{k=1}^Kp_k\mathcal{N}(x_i|\mu_k,\Sigma_k)$

• $Q=\sum\limits_{k=1}^K\sum\limits_{i=1}^N[\log p_k + \log \mathcal{N}(x_i|\mu_k,\Sigma_k)]p(z_i=k|x_i,\theta^t)$

• 极大似然需要计算 $$P(X)$$，EM 计算 $$P(X,Z)$$。$$P(X) = \sum _Z P(X,Z)$$，每次单独考虑 $$P(X,Z)$$，避免在 log 中求和。

E 和 M 具体的含义还没有整理！

影响模型的收敛速度和模型质量。

[[Batch Normalization]] 可以有效降低深度网络对 weight 初始化的依赖。非线性计算之前，输出值有较好的分布。BN 强行将输出值做一次高斯变换和线性变换。

常量初始化

高斯分布初始化

• tf.truncated_normal 按两倍标准差截断

• tf.random_normal

[[正交初始化]]

不同方法的均值和方差

• [[He Initialization]] :<-> 0 均值，标准差为 sqrt(2 / fan_in)
• [[Xavier Initialization]] :<-> 0 均值，标准差为 sqrt(2 / (fan_in + fan_out))
  card-last-score:: 5
  card-repeats:: 1
  card-next-schedule:: 2023-07-23T14:52:57.521Z
  card-last-interval:: 4

See Also

• [[神经网络参数全部初始化为0]] 不可行

Ref

• 聊一聊深度学习的weight initialization - 知乎

结构

• 遗忘门 forget gate :<-> $\Gamma_f^{\langle t\rangle}=\sigma\left(W_f\left[a^{\langle t-1\rangle}, x^{\langle t\rangle}\right]+b_f\right)$

  • 取值范围在 0 到 1

  • 功能 :-> 控制上一个 cell 的状态 $c^{t-1}$，有多少信息进入当前状态 $c^{t}$

• 更新门 update gate :<-> $\Gamma_u^{\langle t\rangle}=\sigma\left(W_u\left[a^{\langle t-1\rangle}, x^{\langle t\rangle}\right]+b_u\right)$

  • 功能 :-> 控制输入 $x$，有多少信息进入当前状态 $c^{t}$

• $\tilde{c}^{(t)}$ :-> $\tilde{c}^{(t)}=\tanh \left(W_C\left[a^{\langle t-1\rangle}, x^{\langle t\rangle}\right]+b_C\right)$

• $c^{\langle t\rangle}=\Gamma_f^{\langle t\rangle} \circ c^{(t-1\rangle}+\Gamma_u^{\langle t\rangle} \circ \tilde{c}^{\langle t\rangle}$

• 输出门 output gate :<-> $\Gamma_o^{(t)}=\sigma\left(W_o\left[a^{\langle t-1\rangle}, x^{\langle t\rangle}\right]+b_o\right)$

  • 作用 :-> 控制当前状态 $c^{t}$ 有多少信息进入 cell 的输出

• 新的 $a^{\langle t\rangle}$ 计算方式:-> $a^{\langle t\rangle}=\Gamma_o^{\langle t\rangle} \circ \tanh \left(c^{\langle t \rangle}\right)$
  
  occlusion:: eyIuLi9hc3NldHMvaW1hZ2VfMTcyMzk5MDQxOTk3NF8wLnBuZyI6eyJjb25maWciOnsiaGlkZUFsbFRlc3RPbmUiOnRydWV9LCJlbGVtZW50cyI6W3sibGVmdCI6MzQwLjM5MDM4Mjc3MTYxMjA1LCJ0b3AiOjUxMS4yNzA4NDgyMjA0NTgsIndpZHRoIjoxMjYuNjQzNDg4NDM3ODk3MDIsImhlaWdodCI6NjAuMDcwNzg4OTk5NzMzMzk1LCJhbmdsZSI6MCwiY0lkIjoxfSx7ImxlZnQiOjY5Mi40NDI4NTY5OTEyMDIsInRvcCI6NTE3LjU3MDYzMjMyMDcxMzgsIndpZHRoIjoxMjcuNDkxNDkxMTY5MTE0NDEsImhlaWdodCI6NDQuOTcyNzM1NDkzOTk5MzksImFuZ2xlIjowLCJjSWQiOjV9LHsibGVmdCI6NDc2LjQ4NTUyNjQ2MDQ5OTU2LCJ0b3AiOjUxNi42NjU2NTUyNzI5MSwid2lkdGgiOjEzNC40MzQ1MTUwMDAxMzgwNSwiaGVpZ2h0Ijo1MS43Nzk2NjAyMDAwNTE0NywiYW5nbGUiOjAsImNJZCI6Mn0seyJsZWZ0Ijo3OTUuODU2NzMwODU0NTY1NiwidG9wIjoxMzUuNjE0NDIxMjgxNjY2ODYsIndpZHRoIjoxNTUuNjQ4MDYwNDk5MTg2MzksImhlaWdodCI6NjkuMzMzNTA3MjI2MzI1MiwiYW5nbGUiOjAsImNJZCI6M30seyJsZWZ0Ijo1ODEuNzEzNzUzODYzODIxOSwidG9wIjo1MTQuMDExODM4MzkxMzAwOSwid2lkdGgiOjY2LjQ2ODU1MDMyMzY3OTc4LCJoZWlnaHQiOjQ5LjU5MTgzODA0NzYwMzIzLCJhbmdsZSI6MCwiY0lkIjo0fSx7ImxlZnQiOjMwNy4zNzU3NTA1OTQxOTE5LCJ0b3AiOjQzOS45ODU2NzIyMjU1NTMsIndpZHRoIjo4MC4xODAyNjA1ODQ2OTQ5NSwiaGVpZ2h0Ijo1NS4yMzA1MDc5ODE0MzQwNywiYW5nbGUiOjAsImNJZCI6Nn0seyJsZWZ0Ijo0NTguMTE3ODI1NzAyNjgwOTMsInRvcCI6NDUyLjQyNTUwMDc4ODk2NTgsIndpZHRoIjo1MS4xNzc5MjQ4MjcxOTY5OSwiaGVpZ2h0Ijo0Ny44NDAyNDc5OTExNjM4MzUsImFuZ2xlIjowLCJjSWQiOjd9LHsibGVmdCI6NTk1LjIzNDc3NTY4MTMwMzYsInRvcCI6NDQ0Ljg2NzUyNjAzMjg4MzgsIndpZHRoIjo1NC40MjU1MDU2NDk3ODg4NywiaGVpZ2h0Ijo0Ny45NjUyODU2NzE5OTQ3MSwiYW5nbGUiOjAsImNJZCI6OH0seyJsZWZ0Ijo2NjMuOTgyNTIzMzQzNzE2NSwidG9wIjo0NzEuNzA1MDM3MzM3MTMyODYsIndpZHRoIjo2Ni45MTk5OTk5MzU2ODU4NCwiaGVpZ2h0IjozNi43NjQ1MTMyNTIyNzM3OSwiYW5nbGUiOjAsImNJZCI6OX0seyJsZWZ0IjoxNDM0LjY2MTY5OTgzOTU4MDcsInRvcCI6NDMxLjg4MjY3Mjk4MDY2MTgsIndpZHRoIjo1MTAuNDI5MTc2MTI1ODU3MSwiaGVpZ2h0Ijo1ODEuMTI3NTA4NzM2NTQyOCwiYW5nbGUiOjAsImNJZCI6M31dfX0=
  使用饱和的非线性函数

• 为什么 :-> 在输入达到一定值后，输出就不会发生明显变化

• [[sigmoid]] 阈值 0-1 :-> 模拟开关的关闭程度，用于各种门

  • 现代神经网络中门控的选择

• [[Tanh]] 阈值 -1 到 1，梯度的阈值为 0~1 :-> 生成记忆

  • 0 中心

  • 输入在 0 附近相比 Sigmoid 函数有更大的梯度

• 为什么不使用 relu :-> 只能输出大于 0 的部分，前向传播容易发生信息爆炸性增长。

Ref

• [[LSTM/Backward]]

• [[LSTM/Question]]

• 为什么LSTM没有办法处理等差数列？ - 知乎 (zhihu.com)

[[Point Wise]]

• 全局相关性

• 没有对先后顺序的优劣做惩罚

• 将 Ranking 算法转化成回归、分类或序列回归

[[Pair Wise]] 二分类

• 多个 pair 排序问题，比较不同文章的先后顺序

• 目标

  • 减少误分类 doc pair 的比例

• 问题

  • 考虑出现的相对位置，但是没有考虑文档在搜索列表中的位置。

    • 排在搜索结果前面的文章更为重要，如果排在靠前的文章出现判断错误，代价明显高于排在后面的文档

  • 不同查询相关文档数量差异大

• 方法

  • RankNet

  • [[GBRank]]

    • $L\left(f ; x_{u}, x_{v}, y_{u, v}\right)=\frac{1}{2}\left(\max \left\{0, y_{u, v}\left(f\left(x_{v}\right)-f\left(x_{u}\right)\right)\right\}\right)^{2}$

      • 关注逆序部分

      • 逆序 loss 为正，正序 loss 为零

[[List Wise]]

• 考虑整体序列，针对 Ranking 评价指标进行优化

• 方法

  • AdaRank

  • SoftRank

  • [[LambdaMART]]

  • LambdaRank

    • 蓝色表示相关文档，右侧的图片中，虽然指标下降，但是从直觉上来说并不好。

指标

• MAP(Mean Average Precision)

  • $$A P=\frac{\sum_{j=1}^{n_{i}} P(j) \cdot y_{i, j}}{\sum_{j=1}^{n_{i}} y_{i, j}}$$

  • $$P(j)=\frac{\sum_{k: \pi_{i}(k)} \leqslant y_{i, k}}{\pi_{i}(j)}$$

  • $$MAP=\frac{\sum_{q=1}^{Q} \operatorname{AveP}(q)}{Q}$$

    • 所有 query 的 ap 值取平均

  • 例子

    • 假设query_1有4个相关的document，分别被模型排在1，2，5，7位，那么query_1的AP就是(1/1+2/2+3/5+4/7) / 4；

query_2有5个相关的document，分别被模型排在2，3，6，29，58位那么query_2的MAP就是(1/2+2/3+3/6+4/29+5/58) / 5，但通常情况下，我们的  不会取到58，只会关注排名靠前的document，因此排在29与58的document可以视为没有被模型检索出来，假设取m  ，则query_2的AP是(1/2+2/3+0+0+3/6+0+0)/5。

  + 对以上两个query取平均即可得出MAP。

• [[NDCG]]

Ref

• Learning to Rank for Information Retrieval

• FM模型在LTR类问题中的应用 [[杨镒铭]]

  • $$L=-\log \left(\tilde{y}_{i j}\right)=\log \left(1+\exp \left(-\left(\tilde{y}\left(x_{i}\right)-\tilde{y}\left(x_{j}\right)\right)\right)\right.$$

逻辑回归，能融合多种特征。

$y=f(W^x+b), y \in \{0, 1\}, f$ 是 link function
线性分类

• 硬分类 :<-> 直接输出输出对应的分类 $y \in \{0, 1\}$

  • 线性判别分析[[Fisher]]

  • [[感知机]]

• 软分类 :<-> 产生不同类别的概率 $y \in [0, 1]$

  • 概率生成式(连续)，类别先验 [[Gaussian Discriminant Analysis]] GDA [[Naive Bayes Classifier]]

    • $P(y=0|x), P(y=1|x)$ 的大小关系

  • 概率判别式(离散) Logisitic Regression

    • 直接对 $$P(Y|X)$$ 建模

逻辑回归

• P(Y|X, \theta)=p_1^yp_0^{1-y}$$ 服从[\[\[Bernoulli Distribution\]\]](/post/logseq/Bernoulli%20Distribution.html) + 求 MLE 转化成 Cross Entropy

• 取 $$z=\ln \frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2}$$

  • 激活函数 [[sigmoid]] $f(z)=\frac{1}{1+exp(-z)} \in (0, 1.0)$

    • 阶跃函数不连续，sigmoid函数光滑，处处可导

    • 数据取值范围从正无穷压缩到 0-1

  • 两类联合概率比值的对数

  • odds 几率代表事件发生和不发生的比值 $$\frac{p}{1-p}$$

  • 对数几率的线性回归

• $$P(y=0|x)=\frac{1}{1+\exp(-w^Tx)}$$

• $$P(y=1|x)=\frac{\exp(-w^Tx)}{1+\exp(-w^Tx)}$$

• MLE $$w=\mathop{argmax} \sum(y_i \log p_1 + (1-y_i)\log p_0)=\mathop{argmax} \sum(y_i \log f(x,w) + (1-y_i)\log (1-f(x,w))$$

  • 等价于 Cross Entropy

• 多分类

  • softmax regression

  • 参数冗余

• 多标签：每个标签设计一个分类器

在推荐系统中，LR 当成是一个分类问题处理，通过预测正样本的概率对物品进行排序。将推荐问题转化为预估问题。另外也能使用 [[Pair Wise]]

优点

• 数学含义：用户是否点击广告是一个经典的掷偏心硬币问题，显然符合伯努利分布

• 可解释性强

• 工程化较为简单

[[面试]]

• LR归一化问题

  • 什么情况可以不归一化 :-> 最小二乘法
  • 什么情况必须归一化 :-> 梯度下降算法
  • [[Wide&Deep]]

• 提到LR损失函数要能知道交叉熵，为什么是它，以它为损失函数在优化的是一个什么东西，知道它和KL散度以及相对熵的关系

• 提到LR的求解方法，比如SGD，知道SGD和BGD的区别，知道不同的GD方法有什么区别和联系，二阶优化算法知道什么，对比offline learning和online learning的区别

• 提到调参，知道模型不同超参数的含义，以及给定一个特定情况，大概要调整哪些参数，怎么调整

• 提到LR的正则，知道l1l2的原理，几何解释和概率解释

• LR的分布式实现逻辑是怎么样的，数据并行和模型并行的区别，P-S架构大概是怎么一回事

• LR作为一个线性模型，如何拟合非线性情况？

  • 特征侧比如离散化，交叉组合，模型比如引入kernel，又可以推广到FM等model上

• LR 如何解决低维不可分

  • 通过核函数将特征从低维空间转换到高维空间，高维空间中线性可分的几率会变高

MSE/MAE/ [[Huber Loss]]

• 假设误差服从某种特定分布，然后通过 MLE 推导最终 loss 形式。

• MSE 反向传播梯度 $-\left(y^{(i)}-\theta^T x^{(i)}\right) x^{(i)}$

  • MSE 梯度容易受到异常值影响。异常样本 label 非常大时，$y^{(i)}-\theta^T x^{(i)}$ 的值也会非常大，将模型带偏。

    • 反过来离群点会影响业务时，应该使用 MSE。

• MAE 反向传播梯度 $-\frac{y^{(i)}-\theta^T x^{(i)}}{\left|y^{(i)}-\theta^T x^{(i)}\right|} x^{(i)}$

  • 使用 MAE 损失时，梯度始终相同。在接近最小值的时候减少学习率。

• MSE 和 MAE （L2 损失和 L1 损失）

  • 1. 平方差更容易求解，绝对误差对离群点更加鲁棒。
  • 2. pb 如果只预测一个值，最小化 MSE 倾向于均值，最小化 MAE 倾向于中位数。对于异常点，中位数比平均值更鲁棒。（简单可以证明）

[[ZILN]] [[Log-Normal Distribution]]

• LTV 分布，首次购买后产生的价值，0 代表只购买一次

• $L_{Z I L N}(x ; p, \mu, \sigma)=-\mathbf{1}_{x=0} \log (1-p)-\mathbf{1}_{x>0}\left(\log p-L_{\text {Lognormal }}(x ; \mu, \sigma)\right)$

  • x 是 label

  • p 预估购买概率

  • 预估金额 $L_{\text {Lognormal }}(x ; \mu, \sigma)=\log (x \sigma \sqrt{2 \pi})+\frac{(\log x-\mu)^2}{2 \sigma^2}$

  • 网络结构

[[Weighted Logistics Regression]] 预估用户观看时长

• 出处 [[@Deep Neural Networks for YouTube Recommendations]]

• [[Cross Entropy Loss]] 正样本以时长为权重，负样本权重为 1。模型能学习到观看视频的时间
  ，reweight 后，改变正负样本的比例。

  • cross entropy 最终预估的概率是正样本的比例。

• label 为 T 的样本，相当于在分类任务重变为 T 个正样本。正样本总体比例变成 $\frac{\sum_{i=1}^k T_i}{N+\sum_{i=1}^k T_i-k}$

  • N 总样本，k 正样本，Ti 每个样本时长

• LR 可以写成

  • $\frac{1}{1+e^{- \text {logit }}}=\frac{\sum_{i=1}^k T_i}{N+\sum_{i=1}^k T_i-k}=\frac{P}{N+P}$

  • $\frac{P}{N}=e^{\text {logit }}$

  • 上面推导如果不忽略 k

    • label为 T 的样本，把它当做 T 个正样本和一个负样本，为每个正样本多增加一个负样本。

    • $\frac{1}{1+e^{-\operatorname{logit}}}=\frac{\sum_{i=1}^k T_i}{N+\sum_{i=1}^k T_i-k+k}$

• reweight 之后相当于假设 label 服从参数为 p 的几何分布（失败概率），label T就是几何分布的 pdf 取 log 后提到前面的值，表示连续失败 T 次。

[[Bucketing with Softmax]] 对 label 的值域进行分桶，根据每个样本的 label 把样本分到某个桶里。回归任务转成多分类问题，使用 softmax 损失函数训练。

• 线上预测时，用 softmax 预估的概率分布对每个桶做加权求和。

  • pred $=\sum_{i=1}^n p_i v_i$

• 如何确定分桶数量和每个桶大小？

  • 目标让每个分桶的样本均衡

• 优化

  • 每个桶再套上 mse 等损失转化成分区间的 multi-task 建模

• 分桶之后会丢失 laebl 之间的大小关系（label=50 分到 [0,10] 或 [51,100] 的损失没有区分性)。引入[[Label Smooth]]

  • 对 label 做变换时，不用 one-hot 而是转化成高斯分布等形式

[[ETA]]

• 均值和中位数哪个大？均值大？

• 对于 badcase 来说，哪个模型效果更好？

• MSE 对异常值更加

• MAPE 没有上界，对异常值敏感，训练出来的模型倾向于低估。（高估带来较大的惩罚）

• SMAPE 有界（0-200），高估和低估的上界都是 200 。

Ref

• 回归任务里的损失函数 | 吴良超的学习笔记 (wulc.me)

基本网络框架 [[底层共享法]]

occlusion:: eyIuLi9hc3NldHMvaW1hZ2VfMTczNjE3NTMyNDk1N18wLnBuZyI6eyJjb25maWciOnt9LCJlbGVtZW50cyI6W3sibGVmdCI6MjY3Ljk5MzU1MDM0NDkxNjksInRvcCI6NjAyLjM4MzAxMDkzMDM5MjIsIndpZHRoIjozNDEuMTMyNDgzNDEzNjAxLCJoZWlnaHQiOjg3LjIzMzk3ODEzOTIxNTc2LCJhbmdsZSI6MCwiY0lkIjoxfSx7ImxlZnQiOjEyODcuMTM3ODQyNzI5Nzg5LCJ0b3AiOjYwMy44MTA5NTY5NDUzNjkzLCJ3aWR0aCI6Mjk5Ljk5MDY0NDI5MTI0MjIzLCJoZWlnaHQiOjg0LjM3ODA4NjEwOTI2MTI4LCJhbmdsZSI6MCwiY0lkIjoxfV19fQ==
结构

• [[MMoE]]

• CGC

• ESSM

• [[PLE]]

Optimization

• Gradnorm

  • 考虑 Loss 量级和考虑不同任务的速度

  • Label loss 和 Gradient loss

• Dynamic Weight Averaging

两大分支：“网络设计” 以及 “损失函数设计”

关键点

• 任务需要有相关性

• 任务之间可以共享低层表示

网络设计

• TODO 参考 [[神经网络与深度学习]]

• 网络如何小巧轻便，如何最大幅度的让不同的任务去共享信息。

• Hard parameter sharing 底层共享参数，最上层有不同的任务。

  • Task 越多，单任务越不容易拟合

  • 底层难以学到试用于所有任务的表达，比如多任务：猫狗分类，猫汽车分类

• Soft parameter sharing

  • 不同任务的参数空间需要添加限制，不然容易变成 single task learning

• 层次共享

  • 图像中不同层次的表达能力不同：结构提取、语义提取

• 共享-私有

• Cross-Stitch Network、Multi-Attention Network、AdaShare、MTL+NAS 可以参考 “综述性质的文章Multi-task Learning and Beyond: 过去，现在与未来 - 知乎”

损失函数设计

• 如何分配不同任务损失函数的权重？

类似方向 [[Auxiliary learning]]

[[Ref]]

• DMS降本增效新方案——视觉多任务模型-Way社区 (xiaojukeji.com)

• DONE [[@深度学习的多个loss如何平衡？]]

• 综述性质的文章Multi-task Learning and Beyond: 过去，现在与未来 - 知乎

• [[@蘑菇街首页推荐多目标优化之reweight实践：一把双刃剑？]]

• 综述 Multi-Task Learning for Dense Prediction Tasks

• 多任务学习-Multi-Task-Learning

• [[@推荐精排模型之多目标模型]]

$\hat{y}_{N F M}(\mathbf{x})$ :-> $w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+f(\mathbf{x})$

• 第一项和第二项是线性回归

• 引入第三项神经网络学习 :-> 数据之间的高阶特征

  • 网络输入 :-> FM 模型的二阶特征交叉结果
  • 与直接使用高阶 FM 模型相比 :-> 可以降低模型的训练复杂度，加快训练速度。
    NFM 的神经网络部分包含 4 层，分别是 Embedding Layer、Bi-Interaction Layer、Hidden Layers、Prediction Score。

tags:: #[[Model Architecture]]

Embedding Layer 层对输入的稀疏数据进行 Embedding 操作。最常见的 Embedding 操作是在一张权值表中进行 lookup ，论文中作者强调他们这一步会将 Input Feture Vector 中的值与 Embedding 向量相乘。

Bi-Interaction Layer 层是这篇论文的创新，对 embedding 之后的特征两两之间做 element-wise product，并将结果相加得到一个 k 维（Embeding 大小）向量。这一步相当于对特征的二阶交叉，与 FM 类似，这个公式也能进行化简：

• $f_{B I}\left(\mathcal{V}_{x}\right)=\sum_{i=1}^{n} \sum_{j=i+1}^{n} x_{i} \mathbf{v}_{i} \odot x_{j} \mathbf{v}_{j} =\frac{1}{2}\left[\left(\sum_{i=1}^{n} x_{i} \mathbf{v}_{i}\right)^{2}-\sum_{i=1}^{n}\left(x_{i} \mathbf{v}_{i}\right)^{2}\right]$
  Hidden Layers 层利用常规的 DNN 学习高阶特征交叉

Prdiction Layer 层输出最终的结果：

实验结果：  tags:: #HOFM

解决 [[Internal Covariance Shift]]

• 本质是平滑 Loss，保持在梯度下降过程中的稳定。

连续特征的值分布不统一，会导致训练波动，影响收敛速度。
归一化：对不同特征维度的伸缩变换的目的是使各个特征维度对目标函数的影响权重是一致的，即使得那些扁平分布的数据伸缩变换成类圆形。

[[归一化方法]]

减少人为参数选择

缓解过拟合

减少梯度消失，加快收敛速度，提高训练精度

通过计算均值和方差的集合分成，输入 [N, C, H, W] 维度图片

• 不同方法的区别在于神经元集合 S 的范围如何确定

• [[Group Normalization]]

• [[Batch Normalization]] 神经网络中间层进行归一化

  • C 维度上，计算 (N, H, W) 的统计量

• [[Layer Normalization]] RNN 等序列模型

• [[Instance Normalization]]

  • 与 LN 相同对单个样本操作

  • IN 对同一层神经元中的同一个通道进行归一化

[[Weight Normalization]]

Ref

• 详解深度学习中的Normalization，BN/LN/WN - 知乎

为什么使用

如何理解Transformer论文中的positional encoding，和三角函数有什么关系？ - 知乎 (zhihu.com) #card

• 如何构建一种位置编码？

  • 直接使用下标计数 PE= pos

    • 序列没有上限，后面的词可能位置编码非常大。

  • 使用文本长度对每个位置归一化 PE = pos/(T-1)

    • 不同长度文本的位置编码步长是不同的，长文本和短文本中两个相邻词的位置编码存在差异

  • 有界周期函数

• 本质对位置信息进行建模，需要满足

  • 需要体现同一个单词在不同位置的区别

  • 相对次序关系，体现先后次序关系，编码差异不应该依赖于文本长度

  • 值域落在一定数值区间内

Ref

• Transformer升级之路：1、Sinusoidal位置编码追根溯源 - 科学空间|Scientific Spaces

occlusion:: eyIuLi9hc3NldHMvaW1hZ2VfMTcyNzEwMTQwODE4OV8wLnBuZyI6eyJjb25maWciOnsiaGlkZUFsbFRlc3RPbmUiOnRydWV9LCJlbGVtZW50cyI6W3sibGVmdCI6MTU0NC4wNzUyNzMzNjA3MzQ0LCJ0b3AiOjUwMC42NTQzNTc4NTAwMzkxLCJ3aWR0aCI6NzIyLjE0MDMwMTkxMDIxMzEsImhlaWdodCI6MTA3LjMwMjU3NDYzMDExODY3LCJhbmdsZSI6MCwiY0lkIjoxfSx7ImxlZnQiOjE0NjUuNTcxNzQ2MTMzNjQ4NSwidG9wIjo2MTYuNjU1MTg4MjQ2MjkxNiwid2lkdGgiOjU1OS4xNDU3NzEwOTM3ODQ2LCJoZWlnaHQiOjk5LjMwMzA3NjczMDE3ODMsImFuZ2xlIjowLCJjSWQiOjJ9LHsibGVmdCI6NzAzLjQ4OTk5OTUyMTU3MjgsInRvcCI6Mzk2LjI5NzA3MzY4NDQxODI1LCJ3aWR0aCI6ODIuMDIwNTAzNjg3MzcxODQsImhlaWdodCI6NzEuNTY1NDQ4ODQ0OTE0MjMsImFuZ2xlIjowLCJjSWQiOjN9LHsibGVmdCI6ODI1LjUzMjQzMjk1ODM4MTMsInRvcCI6MTMxLjk4MTg1NjMyMTg0MjEsIndpZHRoIjoxNDcuODE2MDUxNjczNjU5MSwiaGVpZ2h0Ijo3MC44MDQyOTIyNzcyMjA3LCJhbmdsZSI6MCwiY0lkIjoyfV19fQ==
$h_{t}=\tanh \left(W x_{t}+U h_{t-1}+b\right)$

• $\frac{d h_{t}}{d \theta}=\frac{\partial h_{t}}{\partial h_{t-1}} \frac{d h_{t-1}}{d \theta}+\frac{\partial h_{t}}{\partial \theta}$

  • $|\frac{\partial h_{t}}{\partial h_{t-1}}| >1$，导致 :<-> 梯度爆炸
    • 如何解决 :-> 梯度裁剪
  • $|\frac{\partial h_{t}}{\partial h_{t-1}}| < 1$，导致 :<-> 梯度消失
    $\frac{\partial h_{t}}{\partial h_{t-1}}=\left(1-h_{t}^{2}\right) U$

• 结合 $h_{t}=\tanh \left(W x_{t}+U h_{t-1}+b\right)$
  对应的曲线

  • 为什么隐状态激活函数使用 [[Tanh]] 而不是 [[ReLU]]？
    • 为什么用 Tanh :-> $\frac{\partial h_{t}}{\partial h_{t-1}}$ 是有界的，可以缓减梯度爆炸的风险。
    • 为什么不用 ReLU :-> 正半区没有上限
      • 将 U 初始化在单位矩阵附近 + 梯度裁剪也可以得到不错的效果

• 如果 U 很大，ht 会接近于 1，$$\frac{\partial h_{t}}{\partial h_{t-1}}$$ 反而会小
  [[RNN/Backward]]

[[Ref]]

• [[RNN/Question]]

• [[LSTM]]

• [[GRU]]

• 6_RNN

• 也来谈谈RNN的梯度消失/爆炸问题 - 科学空间|Scientific Spaces

单纯堆积卷积层，并不能让模型表现的更好。

vanishing/exploding gradients

离输入近的网络层会产生梯度消失现象，比较难训练，接到靠近输出的层。
使用 Residual Block

Deep Residual Learning for Image Recognition

• 学习 residual mapping 比 original unreferenced mapping 轻松

• identity mapping 给模型提供 shortcuts，如果 block 前后输入输出大小不同，可以通过 w 参数转化

• 在加法之后过第二个非线性单元

• bottleneck architectures

• 为了解决层数变多时，参数数量增加问题。通过 bottleneck 结构，减少维持和左边相同的参数量，然后网络变成 3 层

[[Identity Mappings in Deep Residual Networks]]

[[Residual Networks Behave Like Ensembles of Relatively Shallow Network]]

[[ResNet/Question]]

[[Ref]]

• 残差网络解决了什么，为什么有效？ - 知乎

• 给妹纸的深度学习教学(4)——同Residual玩耍 - 知乎 里面有解释 ResNet 的 ReLU 放在哪里的原因

• 对ResNet本质的一些思考 - 知乎 (zhihu.com)

Layer Normalization

On Layer Normalization in the Transformer Architecture

• PostLN

{{embed [[2020/09/22]] 堵点
}}

Informer：把残差转移到Attention矩阵上面去 - 科学空间|Scientific Spaces

• Which Training Methods for GANs do actually Converge?

  • 残差每一步累积导致方差很大从 $$x+f(x)$$ 变成 $$x+\alpha f(x)$$

每次迭代只采样一个样本

优化 learn-rate，自适应学习率

• 自适应学习率的方法：对不同的参数使用不同的学习率，参数更新频率和更新步长负相关

• [[Annealing]]，全局共享learn_rate 所有的参数以相同的幅度进行更新

  • 随步衰减

  • 指数衰减

  • 1/t衰减

• [[AdaGrad]]，参数独立 learn_rate 更新幅度取决于参数本身

  • $\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{G_t+\epsilon}} \odot g_t$

  • $n_t=n_{t-1}+g^2_t$

  • $\Delta \theta _t = -\frac{\eta}{\sqrt{n_t+\epsilon}}$

  • 计算一个时间区间内的梯度值累积和 [[移动平均]]

    • AdaDelta 分母滑动区间 + 单位矫正

      • $E\left[g^2\right]_t=\gamma E\left[g^2\right]_{t-1}+(1-\gamma) g_t^2$

      • $E\left[\Delta \theta^2\right]_t=\gamma E\left[\Delta \theta^2\right]_{t-1}+(1-\gamma) E\left[\Delta \theta^2\right]_t$

      • $\Delta \theta_t=-\frac{R M S[\Delta \theta]_{t-1}}{R M S[g]_t} g_t$

    • [[RMSProp]] 分子滑动区间

      • cache = decay_rate * cache + (1 - decay_rate) * dx**2

      • x += - learning_rate * dx / (sqrt(cache) + eps)

      • $E\left[g^2\right]_t=0.9 E\left(g^2\right)_{t-1}+0.1 g_t^2$

      • $\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{E\left[g^2\right]_t+\epsilon}}$

      • [[Adam]] 分子动量版

        • $v_t=\beta_2 v_{t-1}+\left(1-\beta_2\right) g_t^2$

        • $m_t=\beta_1 m_{t-1}+\left(1-\beta_1\right) g_t$

        • $\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{\hat{v}_t+\epsilon}} \hat{m}_t$

        • [[AdamW]] 和 [[LazyAdam]]

优化梯度方向，减小震荡

• [[Momentum]]：强化相关方向的训练和弱化无关方向的震荡来加速 SGD 收敛

  • $v_t=\gamma v_{t-1}+\eta \nabla_\theta J(\theta)$

  • V[t+1] = rho * v[t] + dx;

  • x[t+1] = x[t] - learningRate * V[t+1]

• Nesterov 梯度加速法

  • 预判前方地形

  • $v_t=\gamma v_{t-1}+\eta \nabla_\theta J\left(\theta-\gamma v_{t-1}\right)$

梯度下降法 [[SGD]]

• 并行化，Scalable

  • Downpour SGD

  • Hogwild!

TODO [[Sequence to Sequence Learning with Neural Networks]]

[[Massive Exploration of Neural Machine Translation Architectures]]

TODO google/seq2seq: A general-purpose encoder-decoder framework for Tensorflow

Encoder - Decoder

Decoder

• decoder 涉及输入是正确的单词还是预测的单词

  • Free Running :-> 使用 Decoder 上一步的预测结果作为当前步的输入

    • 错误累积 :-> 每次输入预测单词，某个单词预测错，后面会跟着错，模型很难收敛

  • [[Teacher Forcing]] :-> 使用目标文本的“标准答案”作为Decoder的输入

    • 缺点 #card

      • 每次输入正确单词，会导致 overcorrect

      • exposure bias 误差爆炸/曝光误差 (训练环节和预测环节存在行为差异)

  • Scheduled sampling 计划采样 #card

    • 1-p 的概率用 teacher forcing

    • 以一定概率随机选择用模型输出还是用真值，选择概率随着训练的推进不断调整

• [[Beam Search]] 每一步，多选几个作为候选，最后综合考虑，选出最优的组合。

[[Transformer]] 不适用 RNN

CNN Seq2Seq [[Convolutional Sequence to Sequence Learning]]

标准化的前提假设

• 数据的权重相同

• 某些算法默认数据的 std=1 mean=0

不适合情况

• 类型不合适，类别变量

• 压缩的数据，稀疏矩阵

什么数据适合标准化？

• SVM RBF

• L1 L2 规则化的线性模型

标准化后损失什么信息？

• 原来的均值和标准差信息

• 含有极端异常点的删u

标准化 [[Standardization]]

• z-score 规范化

  • 将数值范围缩放到0附近, 但没有改变数据分布。

  • $$z=\frac{x-\mu}{\sigma}$$

• 对数据的分布的进行转换，使其符合某种分布（比如正态分布）的一种非线性特征变换

• 消除数量级对于模型的影响。

• 线性模型中，需要学习一条直线区分数据，将原始数据分布中心移动后，只是移动直线。不加正则的情况下。

什么时候需要标准化

• 主要看模型是否具有伸缩不变性。

• 有些模型在各个维度进行不均匀伸缩后，最优解与原来不等价，例如SVM。对于这样的模型，除非本来各维数据的分布范围就比较接近，否则必须进行标准化，以免模型参数被分布范围较大或较小的数据dominate。

• 有些模型在各个维度进行不均匀伸缩后，最优解与原来等价，例如logistic regression。对于这样的模型，是否标准化理论上不会改变最优解。但是，由于实际求解往往使用迭代算法，如果目标函数的形状太“扁”，迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型，最好也进行数据标准化。

• TCN 中输入和输出可能有不同的宽度，c 图表示使用 11 卷积调整输入大小

  • 也可以直接通过 zero padding 来增加 channels

TCN = 1D FCN + causal convolutions

特点

• 使用因果卷积，不会泄漏未来信息。

  • 论文中强调和 RNN 之类方法进行对比，所以要考虑因果。

• 可以取任意长度的序列，并将其映射到相同长度的输出序列。

• 引入 [[ResNet]] 和扩张卷积的组合可以将网络做深以及增加感受野。

细节

• tcn 中没有 pooling 层

• normalization 方法是 weight norm，更适合序列问题

增加感受野的方法

• 更大的 kernel_size (增加参数，卷积核大效果差，卷积核过大会退化成一个全连接层)

• [[空洞卷积]]

时序问题

• 1. 输入和输出矩阵大小相同
• 2. 不能使用没有发生时刻的信息，因果卷积

[[ETA 模型]] 实现

• tf.nn.conv1d(input, filters, stride, padding, data_format='NWC', dilations=None, name=None)

[[Web Traffic Time Series Forecasting 1st place solution]]

两种方法

• Count-based

  • word frequency and co-occurrence matrix

• Context-based

词向量常用方法

• [[One-hot Encoding]] 简单

• Distributed representaion：包含信息多

[[One-hot Encoding]] 维度灾难，样本稀疏

统计语言模型：通过统计词频计算一个句子在文本中出现的概率，以此确定哪个词序列的可能行更大。

• [[Markov]]假设 n-gram 模型

• 泛化能力差、模型计算复杂度高、没有解决文本本身的表征问题

[[NNLM]] 利用神经网络求解出每个词语的 Word Embedding

[[Word2Vec]] 考虑文本的上下文环境

[[GloVe]] svd 矩阵分解和 [[Word2Vec]] 上下文思想

Conxtextualized Word Embedding 每一个 word token 都给一个 embedding

[[ELMo]]

[[GPT]] 单向语言模型，生成式任务

[[BERT]]

常见 emebdding 方法对比

[[Ref]]

• 文章 - WordEmbedding考古

Glorot 条件 :-> 好的初始化应该使得各层的激活值和梯度的方差在传播过程中保持一致。

• mean=0.0， std_dev=(2.0 / (input_dim + output_dim)) ** 0.5

• tf.contrib.layers.xavier_initializer

• W = tf.Variable(np.random.randn(node_in, node_out)) / np.sqrt(node_in)

保持输入与输出的方差一致。在线性函数上推导出来，部分非线性函数比如（tanh）也可以使用。ReLU 需要使用 [[He Initialization]] 解决

Ref

• 初始化方法 - Keras中文文档

先验知识以及假设

• 算法对学习问题做的假设

归纳偏置

• 归纳和演绎 induction deduction

• 从一些例子中寻找共性、泛化，形成一个比较通过的规则的过程

• 偏置代表对模型的偏好

• 用规则约束模型，从而起到模型选择

  • 将无限可能的目标函数约束在一个有限的类别假设中

  • 近似损失 + 估计损失(更宽松的假设会增大这个损失)

常见的例子

• [[奥卡姆剃刀]] :-> 希望学习到的模型复杂度更低

• [[KNN]] :-> 特征空间中相邻的样本倾向于属于同一类

• SVM 好的分类器 应该 最大化类别边界距离

• [[RNN]] :-> 每一个时刻的计算依赖历史计算结果

  • sequentiality

  • time invariance

    • 序列顺序上的 timesteps 有联系

  • 时间变换不变性

    • 权重共享

• 双向 RNN

  • RNN 假设当前输入和之前的输入有关系，双 RNN 假设当前输入和之前、之后的输入都有关系

• [[DNN]] :-> 信息应该逐级加工，层层抽象

• [[CNN]] :-> 信息具有空间局部性，滑动卷积共享权重方式降低参数空间

  • locality

  • spatial invariance

    • 空间相近的 grid elements 有联系而远的没有

  • 空间变换不变性 translation invariant

    • kernel 权重共享

• [[GNN]] 连接不变性

• [[Attention]]

• [[Word2Vec]] :-> A word’s meaning is given by the words that frequently appear close-by.

  • 结构相似性

  • 例子：猫和狗在语料中没有同时出现，但是他们的上下文完全一致，所以最终 embedding 相似。

    • 我有一只猫。

    • 我有一只狗。

不同部分作用

• query :-> 与 key 计算相似度，为自身的输出 i 建立权重
• key :-> 与 query 计算相似度，建立第 j 个向量 j 的权重
• value :-> 作为加权总和的一部分，计算每个输出向量
  对自身 $$X$$ 线性变化得到 $$Q=W_QX, K=W_KX, V=W_VX$$，用来捕获同一个句子中单词之间的一些句法特征或者语义特征。

注意力计算

• $$\begin{aligned} \mathbf{h}_{i} &=\operatorname{att}\left((K, V), \mathbf{q}_{i}\right) \\ &=\sum_{j=1}^{N} \alpha_{i j} \mathbf{v}_{j} \\ &=\sum_{j=1}^{N} \operatorname{softmax}\left(s\left(\mathbf{k}_{i}, \mathbf{q}_{i}\right)\right) \mathbf{v}_{j} \end{aligned}$$

打分函数 $${H=V softmax(\frac{K^TQ}{\sqrt{d_3}})}$$

过程

为什么 self-attention 先对 embedding 进行 dense 层映射，然后再进行 attention 计算？

• dense 层 #card

  • W 为自注意力层提供一些可控制的参数，允许输入的向量适合 QKV 的功能。

  • qkv 的大小，实现降维。

  • 多头机制作用 :-> 每一个头对应的 wq、wk、wv 矩阵都不同，对模型的本身特征抽取的多样性具有帮助。

• 为什么不能直接做 attention 计算？原始 embedding 空间点击建模 :-> 语义关系

  • 点积建模语义的问题 :-> 默认假设语义相近的注意力更高， VVV 中自己对自己的注意力权重永远最高

    • 结果 :-> 其他位置上有关系的注意力相关性就会被弱化。

• 进行变换后的点积含义

  • 新空间点积 :-> 表示注意力高，但不代表语义相似度高。
    • 好处 :-> 能在新空间里更加专注于注意力的学习。

• 一个词在做 query、key、value 时，直觉 :-> 有不同的表示

为什么 self-attention 中的词向量要乘以 QKV 参数矩阵？

• self-attention 核心利用 文本中的其它词 来增强 目标词的语义表示
• 不乘以 QKV 矩阵 :-> qkv 完全一样，qi 和 ki 的点积比重会最大，无法有效利用上下文信息来增强当前词的语义表示。
• QKV 参数矩阵使得多头作用 :-> 类似于 CNN 中的多核，使捕捉更丰富的特征/信息成为可能
  现在看来self-attention 是增强了模型表示能力，还是有了更好的对特征的权重加权？ - 知乎 :-> 增强模型表达能力
• 增强模型表达能力 :-> 加权对象是 token，融合不同的 token 来构造当前 token 在当前上下文情况下的表示
• 如果是对特征进行加权， :-> 初始化的 word embedding应该直接用那些预训练好的，实际上预训练的词向量并不会提高模型收敛后的效果。

Ref

• Transformers from scratch | peterbloem.nl

• 关于attention机制的一些细节的思考 - 知乎 (zhihu.com)

  • 为什么 self-attention 先对 embedding 进行 dense 层映射，然后再进行 attention 计算？

seq2seq使用teacher forcing有一个问题，就是模型训练和预测行为的不一致会导致模型的泛化性能下降

[[Transformer]] 训练阶段使用这种方式，旨在提升序列模型训练稳定性、加速模型收敛。

• 一次性输入全部目标序列，可以并行的方式一次性输出完整的目标序列，提高训练效率

平稳性

• 存在某种周期、季节性及趋势的方差和均值不随时间变化

• 从统计学角度，平稳性要求对于一个时间序列的取值满足一个确定的分布

平稳性是时间序列分析的基础

• 如果一个时间序列是不平稳的，需要通过 差分 的方式将其转化为平稳时间序列。
  严平稳 strictly stationary

• 时间序列中任意给定长度的两段子序列都满足相同的联合分布

弱平稳 weakly stationary

• 时间序列满足均值平稳性 stationary in mean 和二阶平稳性 secondary order stationary

• 时间序列 $$r_t$$ 满足下面两个条件，则它是弱平稳的

  • 对所有时刻 t，有 $E[r_t] = \mu$，其中$\mu$是常数。
  • 对于所有时刻 t 和任意时间间隔 k，$r_t$ 和 $r_{t-k}$ 的协方差 $\sigma(r_t, r_{t-k}) =\gamma _k$, $\gamma _k$ 与 t 无关，仅依赖于时间间隔 k。

• 方差平稳性 stationary in variance

  • 当 k=0 $\sigma(r_t, r_{t}) =\gamma _t$, $\gamma _t$ 是一个与时间 t 无关的常数且不随时间变化。

• 关于 对所有时刻 t，有 $E[r_t] = \mu$，其中$\mu$是常数。
  的例子

  • 假设指数的日收益序列满足弱平稳条件，对于某一天指数日收益的期望可以用前一段时间的收益期望来近似估计。

• 平稳的随机过程 stationary stochastic process

非平稳性

• 非平平稳数据会导致虚假回归，表现为两个没有任务因果关系的变量，却有很高的相关性

[[ADF 检验]] :<- 判断时间序列是否满足平稳性要求

• 特殊时间序列

  • 时间序列 ${w_t, t=[1,n]}$，$w_t$ 满足均值 0 方差为 $\sigma^2$([[正态分布]])，且对于任意的 k>0，[[自相关]]系数均为 0，则称该时间序列为一个离散的白噪声。

    • $X_t=w_t, w_t\left(0, \sigma^2\right)$

  • 时间序列 $x_t$，满足 $x_t=x_{t-1}+w_t$ ，$w_t$ 是一个均值 0 方差为 $\sigma^2$ 的白噪声，则序列 $x_t$ 为一个随机游走。

    • $X_t=X_{t-1}+w_t, X_t\left(0, t \sigma^2\right)$

• 思想

  • 基于随机游走，对 Xt 回归，如果发现 p=1，说明该序列满足随机游走，就是非平稳的。

    • $\rho_k=\frac{\operatorname{Cov}\left(r_t, r_{t-k}\right)}{\sigma_{r_t} \sigma_{r_{t-k}}}=\frac{\operatorname{Cov}\left(r_t, r_{t-k}\right)}{\sigma_{r_t} \sigma_{r_t}}=\frac{\gamma_k}{\gamma_0}$，利用弱平稳的性质

    • $X_t=X_{t-1}+u_t$ 随机游走，非平稳

    • $X_t=p X_{t-1}+u_t$ 如果 p=1，则 Xt有一个单位根

• from statsmodels.tsa.stattools import adfuller as ADF

  • ADF 函数计算结果

    • 第一个参数 T检验，假设检验值。

    • 第二个参数，P-value，假设检验结果。

    • 第五个参数，不同程度拒绝原假设的统计值

• 如何判断是否平稳

  • ADF 假设检验值同时小于 1% 5% 10% 不同程度拒绝原假设的统计值，说明非常好地拒绝该假设

    • 原假设存在单位根

    • 统计值小于 1%，认为拒绝原假设，该序列是平稳的。

  • [[P-value]] 是否非常接近 0

Ref

• 写给你的金融时间序列分析：基础篇 - 知乎 (zhihu.com)

[[平稳性]] 是时间序列分析的基础，通过 [[ADF 检验]] 判断时间序列是否满足平稳性的要求。

[[时间序列预测/基本数学概念]] 介绍自协方差、自相关系数、偏自相关系数等概念。

[[时间序列预测/评价指标]]有 [[R2 score]]、MAE、MAPE、SMAPEWMAPE 等。

[[传统时间序列预测]]以 AR、MR、ARMA、ARIMA 等序列自回归方法为主。

[[深度学习时间序列预测]]

• [[Time Series Transformer]]

• [[@Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting]]

[[时间序列特征工程]] 三个方向： 时间戳衍生
， ((6302f9ee-1eb7-47ab-af57-17f933664bcb))， ((6302f9ee-52e1-48af-86b1-4e01ff3a4a64))

• [[时间序列缺失值处理]]

• 建模方式

  • 历史窗口大小

  • 预测点 gap 大小

  • 预测窗口大小

任务分类

• Forecasting step

  • one-step

  • multi-step

• Inputting variables

  • autoregressive

  • covariate

• Outputting

  • Single point

  • Probability

• Forecasting target

  • univariate 单变量

  • multivariate

[[时间序列预测/Ref]]

[[Transformer 是否适合时间序列预测]]

求解凸包、TSP 等问题有一个特点：输出是输入的子集。由于输入序列就是词表（不定长），无法使用传统的 seq2seq 模型去建模。

求解凸包、TSP 等问题有一个特点：输出是输入的子集。由于输入序列就是词表（不定长），无法使用传统的 seq2seq 模型去建模。

[[Abstract]]

• Search Ranking and Recommendations are fundamental problems of crucial interest to major Internet companies, including web search engines, content publishing websites and marketplaces. However, despite sharing some common characteristics a one-size-fitsall solution does not exist in this space. Given a large difference in content that needs to be ranked, personalized and recommended, each marketplace has a somewhat unique challenge. Correspondingly, at Airbnb, a short-term rental marketplace, search and recommendation problems are quite unique, being a two-sided marketplace in which one needs to optimize for host and guest preferences, in a world where a user rarely consumes the same item twice and one listing can accept only one guest for a certain set of dates. In this paper we describe Listing and User Embedding techniques we developed and deployed for purposes of Real-time Personalization in Search Ranking and Similar Listing Recommendations, two channels that drive 99% of conversions. The embedding models were specifically tailored for Airbnb marketplace, and are able to capture guest’s short-term and long-term interests, delivering effective home listing recommendations. We conducted rigorous offline testing of the embedding models, followed by successful online tests before fully deploying them into production.

[[Attachments]]

• Real-time Personalization using Embeddings for Search Ranking at Airbnb-2018.pdf

论文解决问题：

• 数据稀疏情况下如何进行训练？

  • 稀疏 id 聚类处理

• 将 user id 和 listing id 聚合成 user type、listing type

• word2vec 中加入 booked listing 作为 global context

目标函数

$$\underset{\theta}{\operatorname{argmax}} \sum_{(l, c) \in \mathcal{D}_{p}} \log \frac{1}{1+e^{-\mathbf{v}_{c}^{\prime} \mathbf{v}_{l}}}+\sum_{(l, c) \in \mathcal{D}_{n}} \log \frac{1}{1+e^{\mathbf{v}_{c}^{\prime} \mathbf{v}_{l}}}+\log \frac{1}{1+e^{-\mathbf{v}_{l}^{\prime} \mathbf{v}_{l}}}$$

booked listing 是正样本，所以有一个负号。由于只有一项，所以没有 sigma 符号。

原始负采样是在全体样本中随机选择，业务特殊性，在正样本同一市场的样本中负采样。更好能发现同一市场中内部 listing 的差异。

new listing 通过附近 3 个同类型、相似价格的 listing embedding 进行平均。

word2vec 方法本来是无监督的，通过引入 booked listing 以及 reject 信息传递部分监督信息

利用 booked 数据训练时，文章中提到 user type 和 listing type 要在同一个空间，不知道为什么下面要有两个公式，以及 c 的含义是什么？

$$\underset{\theta}{\operatorname{argmax}} \sum_{\left(u_{t}, c\right) \in \mathcal{D}_{b o o k}} \log \frac{1}{1+e^{-v_{c}^{\prime} v_{u_{t[[}}}}]]+\sum_{\left(u_{t}, c\right) \in \mathcal{D}_{n e g}} \log \frac{1}{1+e^{v_{c}^{\prime} v_{u_{t[[}}}}]]$$

$$\underset{\theta}{\operatorname{argmax}} \sum_{\left(l_{t}, c\right) \in \mathcal{D}_{b o o k}} \log \frac{1}{1+e^{-\mathrm{v}_{c}^{\prime} \mathrm{v}_{l_{t[[}}}}]]+\sum_{\left(l_{t}, c\right) \in \mathcal{D}_{\text {neg}}} \log \frac{1}{1+e^{v_{c}^{\prime} \mathrm{v}_{l_{t[[}}}}]]$$

embedding 之间直接对比需要在相同的向量空间。根据上面的计算可以生成一个特征 UserTypeListingTypeSim。

在如何在实时模型中引入 embedding 特征：根据一些规则收集一些 listing，计算这些 listing embedding 的平均值，再和当前排序的 lisitng 计算一个相似度，做为一个特征放到模型中。

如何评估按上面方法生成的 emb sim 特征重要性？利用 GBDT？

[[冷启动]] listing embeddings

• 找方圆 10 英里之内的 3 个最相似的 listing，取 listing embedding 的平均

使用 Embedding 方法要考虑的问题：

• 1. 希望Embedding表达什么，即选择哪一种方式构建语料
• 2. 如何让Embedding向量学到东西
• 3. 如何评估向量的效果
• 4. 线上如何使用